Conic Sections Class 11 MCQs Questions with Answers
Question 1.
The locus of the point from which the tangent to the circles x² + y² – 4 = 0 and x² + y² – 8x + 15 = 0 are equal is given by the equation
(a) 8x + 19 = 0
(b) 8x – 19 = 0
(c) 4x – 19 = 0
(d) 4x + 19 = 0
Answer
Answer: (b) 8x – 19 = 0
Hint:
Given equation of circles are x² + y² – 4 = 0 and x² + y² – 8x + 15 = 0
Now, the required line is the radical axis of the two circles are
(x² + y² – 4) – (x² + y² – 8x + 15) = 0
⇒ x² + y² – 4 – x² – y² + 8x – 15 = 0
⇒ 8x – 19 = 0
Question 2.
The perpendicular distance from the point (3, -4) to the line 3x – 4y + 10 = 0
(a) 7
(b) 8
(c) 9
(d) 10
Answer
Answer: (a) 7
Hint:
The perpendicular distance = {3 × 3 – 4 × (-4) + 10}/√(3² + 4²)
= {9 + 16 + 10}/√(9 + 16)
= 35/√25
= 35/5
= 7
Question 3.
A man running a race course notes that the sum of the distances from the two flag posts from him is always 10 meter and the distance between the flag posts is 8 meter. The equation of posts traced by the man is
(a) x²/9 + y²/5 = 1
(b) x²/9 + y2 /25 = 1
(c) x²/5 + y²/9 = 1
(d) x²/25 + y²/9 = 1
Answer
Answer: (d) x²/25 + y²/9 = 1
Hint: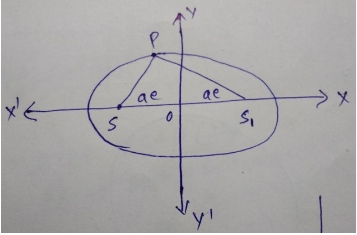
From the question, it is clear that the path traced by the man is an ellipse having its foci at two posts.
Let the equation of the ellipse be
x²/a² + y²/b² = 1
It is given that the sum of the distances of the man from the two flag posts is 10 m
This means that the sum of focal distances of a point on the ellipse is 10 m
⇒ PS + PS1 = 10
⇒ 2a = 10
⇒ a = 5
Again, given that the distance between the flag posts is 8 meters
⇒ 2ae = 8
⇒ ae = 4
Now, b² = a² (1 – e²)
⇒ b² = a² – a² e²
⇒ b² = a² – (ae)²
⇒ b² = 5² – 4²
⇒ b² = 25 – 16
⇒ b² = 9
⇒ b = 3
Hence, the equation of the path is x²/5² + y²/3² = 1
⇒ x²/25 + y²/9 = 1
Question 4.
The center of the ellipse (x + y – 2)² /9 + (x – y)² /16 = 1 is
(a) (0, 0)
(b) (0, 1)
(c) (1, 0)
(d) (1, 1)
Answer
Answer: (d) (1, 1)
Hint:
The center of the given ellipse is the point of intersection of the lines
x + y – 2 = 0 and x – y = 0
After solving, we get
x = 1, y = 1
So, the center of the ellipse is (1, 1)
Question 5.
The parametric coordinate of any point of the parabola y² = 4ax is
(a) (-at², -2at)
(b) (-at², 2at)
(c) (a sin²t, -2a sin t)
(d) (a sin t, -2a sin t)
Answer
Answer: (c) (a sin²t, -2a sin t)
Hint:
The point (a sin²t, -2a sin t) satisfies the equation of the parabola y² = 4ax for all
values of t. So, the parametric coordinate of any point of the parabola y² = 4ax is
(a sin²t, -2a sin t)
Question 6.
The equation of parabola with vertex at origin the axis is along x-axis and passing through the point (2, 3) is
(a) y² = 9x
(b) y² = 9x/2
(c) y² = 2x
(b) y² = 2x/9
Answer
Answer: (b) y² = 9x/2
Hint:
A parabola with its axis along the x-axis and vertex(0, 0) and direction x = -a has the equation:
y² = 4ax ………….. 1
Given, point (2,3) lies on the parabola,
⇒ 3² = 4a × 2
⇒ 9 = 4a × 2
⇒ 9/2 = 4a
From equation 1, we get
y² = (9/2)x
⇒ y² = 9x/2
This is the required equation of the parabola.
Question 7.
At what point of the parabola x² = 9y is the abscissa three times that of ordinate
(a) (1, 1)
(b) (3, 1)
(c) (-3, 1)
(d) (-3, -3)
Answer
Answer: (b) (3, 1)
Hint:
Given, parabola is x² = 9y
Let P(h, k) is the point on the parabola such that abscissa is 3 times the ordinate.
So, h = 3k ……… 1
Since P(h, k) lies on the parabola
So, h² = 9k ……… 2
From equation 1 and 2, we get
(3k)² = 9k
⇒ 9k² = 9k
⇒ 9k² – 9k = 0
⇒ 9k(k – 1) = 0
⇒ k = 0, 1
When k = 0, h = 0
So k = 1
Now, from equation 1,
h = 3 × 1 = 3
So, the point is (3, 1)
Question 8.
The number of tangents that can be drawn from (1, 2) to x² + y² = 5 is
(a) 0
(b) 1
(c) 2
(d) More than 2
Answer
Answer: (b) 1
Hint:
Given point (1, 2) and equation of circle is x² + y² = 5
Now, x² + y² – 5 = 0
Put (1, 2) in this equation, we get
1² + 2² – 5 = 1 + 4 – 5 = 5 – 5 = 0
So, the point (1, 2) lies on the circle.
Hence, only one tangent can be drawn.
Question 9.
In an ellipse, the distance between its foci is 6 and its minor axis is 8 then its eccentricity is
(a) 4/5
(b) 1/√52
(c) 3/5
(d) 1/2
Answer
Answer: (c) 3/5
Hint:
Given, distance between foci = 6
⇒ 2ae = 6
⇒ ae = 3
Again minor axis = 8
⇒ 2b = 8
⇒ b = 4
⇒ b² = 16
⇒ a² (1 – e²) = 16
⇒ a² – a² e² = 16
⇒ a² – (ae)² = 16
⇒ a² – 3² = 16
⇒ a² – 9 = 16
⇒ a² = 9 + 16
⇒ a² = 25
⇒ a = 5
Now, ae = 3
⇒ 5e = 3
⇒ e = 3/5
So, the eccentricity is 3/5
Question 10.
If the length of the tangent from the origin to the circle centered at (2, 3) is 2 then the equation of the circle is
(a) (x + 2)² + (y – 3)² = 3²
(b) (x – 2)² + (y + 3)² = 3²
(c) (x – 2)² + (y – 3)² = 3²
(d) (x + 2)² + (y + 3)² = 3²
Answer
Answer: (c) (x – 2)² + (y – 3)² = 3²
Hint:
Radius of the circle = √{(2 – 0)² + (3 – 0)² – 2²}
= √(4 + 9 – 4)
= √9
= 3
So, the equation of the circle = (x – 2)² + (y – 3)² = 3²
Question 11.
The equation of parabola whose focus is (3, 0) and directrix is 3x + 4y = 1 is
(a) 16x² – 9y² – 24xy – 144x + 8y + 224 = 0
(b) 16x² + 9y² – 24xy – 144x + 8y – 224 = 0
(c) 16x² + 9y² – 24xy – 144x – 8y + 224 = 0
(d) 16x² + 9y² – 24xy – 144x + 8y + 224 = 0
Answer
Answer: (d) 16x² + 9y² – 24xy – 144x + 8y + 224 = 0
Hint:
Given focus S(3, 0)
and equation of directrix is: 3x + 4y = 1
⇒ 3x + 4y – 1 = 0
Let P (x, y) be any point on the required parabola and let PM be the length of the perpendicular from P on the directrix
Then, SP = PM
⇒ SP² = PM²
⇒ (x – 3)² + (y – 0)² = {(3x + 4y – 1) /{√(3² + 4²)}²
⇒ x² + 9 – 6x + y² = (9x² + 16y² + 1 + 24xy – 8y – 6x)/25
⇒ 25(x² + 9 – 6x + y²) = 9x² + 16y² + 1 + 24xy – 8y – 6x
⇒ 25x² + 225 – 150x + 25y² = 9x² + 16y² + 1 + 24xy – 8y – 6x
⇒ 25x² + 225 – 150x + 25y² – 9x² – 16y² – 1 – 24xy + 8y + 6x = 0
⇒ 16x² + 9y² – 24xy – 144x + 8y + 224 = 0
This is the required equation of parabola.
Question 12.
The parametric representation (2 + t², 2t + 1) represents
(a) a parabola
(b) a hyperbola
(c) an ellipse
(d) a circle
Answer
Answer: (a) a parabola
Hint:
Let x = 2 + t²
⇒ x – 2 = t² ……….. 1
and y = 2t + 1
⇒ y – 1 = 2t
⇒ (y – 1)/2 = t
From equation 1, we get
x – 2 = {(y – 1)/2}²
⇒ x – 2 = (y – 1)²/4
⇒ (y – 1)² = 4(x – 2)
This represents the equation of a parabola.
Question 13.
The equation of a hyperbola with foci on the x-axis is
(a) x²/a² + y²/b² = 1
(b) x²/a² – y²/b² = 1
(c) x² + y² = (a² + b²)
(d) x² – y² = (a² + b²)
Answer
Answer: (b) x²/a² – y²/b² = 1
Hint:
The equation of a hyperbola with foci on the x-axis is defined as
x²/a² – y²/b² = 1
Question 14.
The equation of parabola with vertex (-2, 1) and focus (-2, 4) is
(a) 10y = x² + 4x + 16
(b) 12y = x² + 4x + 16
(c) 12y = x² + 4x
(d) 12y = x² + 4x + 8
Answer
Answer: (b) 12y = x² + 4x + 16
Hint:
Given, parabola having vertex is (-2, 1) and focus is (-2, 4)
As the vertex and focus share the same abscissa i.e. -2,
parabola axis of symmetry as x = -2
⇒ x + 2 = 0
Hence, the equation of a parabola is of the type
(y – k) = a(x – h)² where (h, k) is vertex
Now, focus = (h, k + 1/4a)
Since, vertex is (-2, 1) and parabola passes through vertex
So, focus = (-2, 1 + 1/4a)
Now, 1 + 1/4a = 4
⇒ 1/4a = 4 -1
⇒ 1/4a = 3
⇒ 4a = 1/3
⇒ a = /1(3 × 4)
⇒ a = 1/12
Now, equation of parabola is
(y – 1) = (1/12) × (x + 2)²
⇒ 12(y – 1) = (x + 2)²
⇒ 12y – 12 = x² + 4x + 4
⇒ 12y = x² + 4x + 4 + 12
⇒ 12y = x² + 4x + 16
This is the required equation of parabola.
Question 15.
If a parabolic reflector is 20 cm in diameter and 5 cm deep then the focus of parabolic reflector is
(a) (0 0)
(b) (0, 5)
(c) (5, 0)
(d) (5, 5)
Answer
Answer: (c) (5, 0)
Hint: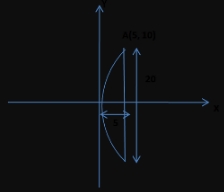
given diameter of the parabola is 20 m.
The equation of parabola is y² = 4ax.
Since this parabola passes through the point A(5,10) then
10² = 4a×5
⇒ 20a = 100
⇒ a = 100/20
⇒ a = 5
So focus of parabola is (a, 0) = (5, 0)
Question 16.
The radius of the circle 4x² + 4y² – 8x + 12y – 25 = 0 is?
(a) √57/4
(b) √77/4
(c) √77/2
(d) √87/4
Answer
Answer: (c) √77/2
Hint:
Given, equation fo the of the circle is 4x² + 4y² – 8x + 12y – 25 = 0
⇒ x² + y² – 8x/4 + 12y/4 – 25/4 = 0
⇒ x² + y² – 2x + 3y – 25/4 = 0
Now, radius = √{(-2)² + (3)² – (-25/4)}
= √{4 + 9 + 25/4}
= √{13 + 25/4}
= √{(13×4 + 25)/4}
= √{(52 + 25)/4}
= √{77/4}
= √77/2
Question 17.
If (a, b) is the mid point of a chord passing through the vertex of the parabola y² = 4x, then
(a) a = 2b
(b) 2a = b
(c) a² = 2b
(d) 2a = b²
Answer
Answer: (d) 2a = b²
Hint:
Let P(x, y) be the coordinate of the other end of the chord OP where O(0, 0)
Now, (x + 0)/2 = a
⇒ x = 2a
and (y + 0)/2 = b
⇒ y = 2b
Now, y² = 4x
⇒ (2b)² = 4 × 2a
⇒ 4b² = 8a
⇒ b² = 2a
Question 18.
A rod of length 12 CM moves with its and always touching the co-ordinate Axes. Then the equation of the locus of a point P on the road which is 3 cm from the end in contact with the x-axis is
(a) x²/81 + y²/9 = 1
(b) x²/9 + y²/81 = 1
(c) x²/169 + y²/9 = 1
(d) x²/9 + y²/169 = 1
Answer
Answer: (a) x²/81 + y²/9 = 1
Hint:
Given a rod of length 12 cm moves with its ends always touching the coordinate axes.
Again given a point P on the rod, which is 3 cm from the end in contact with the x-axis.
It is shown in the figure.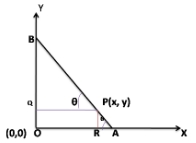
Here AP = 3 cm, AB = 12
Now BP = AB – AP
⇒ BP = 12 – 3
⇒ BP = 9 cm
Again from figure,
∠PAO = ∠BPO = θ (since PQ || OA and are corresponding angles)
Now in ΔBPO,
cosθ = QP/BP
⇒ cosθ = x/9 …………. 1
Again in ΔPAr,
sinθ = PR/PA
⇒ sinθ = y/3 …….. 2
Now square equation 1 and 2 and then add them, we get
cos² θ + sin² θ = x²/81 + y²/9
⇒ x²/81 + y²/9 = 1 (since cos² θ + sin² θ = 1 )
So, the equation of the locus of a point P is x²/81 + y²/9 = 1
Question 19.
The line lx + my + n = 0 will touches the parabola y² = 4ax if
(a) ln = am²
(b) ln = am
(c) ln = a² m²
(d) ln = a² m
Answer
Answer: (a) ln = am²
Hint:
Given, lx + my + n = 0
⇒ my = -lx – n
⇒ y = (-l/m)x + (-n/m)
This will touches the parabola y² = 4ax if
(-n/m) = a/(-l/m)
⇒ (-n/m) = (-am/l)
⇒ n/m = am/l
⇒ ln = am²
Question 20.
The center of the circle 4x² + 4y² – 8x + 12y – 25 = 0 is?
(a) (2,-3)
(b) (-2,3)
(c) (-4,6)
(d) (4,-6)
Answer
Answer: (a) (2,-3)
Hint:
Given, equation fo the of the circle is 4x² + 4y² – 8x + 12y – 25 = 0
⇒ x² + y² – 8x/4 + 12y/4 – 25/4 = 0
⇒ x² + y² – 2x + 3y – 25/4 = 0
Now, center = {-(-2), -3} = (2, -3)








0 Comments