MCQ Questions for Class 11 Maths Chapter 3 Trigonometric Functions with Answers

  

Trigonometric Functions Class 11 MCQs Questions with Answers

Question 1.
The value of cos² x + cos² y – 2cos x × cos y × cos (x + y) is
(a) sin (x + y)
(b) sin² (x + y)
(c) sin³ (x + y)
(d) sin4 (x + y)

Answer

Answer: (b) sin² (x + y)
Hint:
cos² x + cos² y – 2cos x × cos y × cos(x + y)
{since cos(x + y) = cos x × cos y – sin x × sin y }
= cos² x + cos² y – 2cos x × cos y × (cos x × cos y – sin x × sin y)
= cos² x + cos² y – 2cos² x × cos² y + 2cos x × cos y × sin x × sin y
= cos² x + cos² y – cos² x × cos² y – cos² x × cos² y + 2cos x × cos y × sin x × sin y
= (cos² x – cos² x × cos² y) + (cos² y – cos² x × cos² y) + 2cos x × cos y × sin x × sin y
= cos² x(1- cos² y) + cos² y(1 – cos² x) + 2cos x × cos y × sin x × sin y
= sin² y × cos² x + sin² x × cos² y + 2cos x × cos y × sin x × sin y (since sin² x + cos² x = 1 )
= sin² x × cos² y + sin² y × cos² x + 2cos x × cos y × sin x × sin y
= (sin x × cos y)² + (sin y × cos x)² + 2cos x × cos y × sin x × sin y
= (sin x × cos y + sin y × cos x)²
= {sin (x + y)}²
= sin² (x + y)

---

Question 2.
If a×cos x + b × cos x = c, then the value of (a × sin x – b²cos x)² is
(a) a² + b² + c²
(b) a² – b² – c²
(c) a² – b² + c²
(d) a² + b² – c²

Answer

Answer: (d) a² + b² – c²
Hint:
We have
(a×cos x + b × sin x)² + (a × sin x – b × cos x)² = a² + b²
⇒ c² + (a × sin x – b × cos x)² = a² + b²
⇒ (a × sin x – b × cos x)² = a² + b² – c²

---

Question 3.
If cos a + 2cos b + cos c = 2 then a, b, c are in
(a) 2b = a + c
(b) b² = a × c
(c) a = b = c
(d) None of these

Answer

Answer: (a) 2b = a + c
Hint:
Given, cos A + 2 cos B + cos C = 2
⇒ cos A + cos C = 2(1 – cos B)
⇒ 2 cos((A + C)/2) × cos((A-C)/2 = 4 sin²(B/2)
⇒ 2 sin(B/2)cos((A-C)/2) = 4sin² (B/2)
⇒ cos((A-C)/2) = 2sin (B/2)
⇒ cos((A-C)/2) = 2cos((A+C)/2)
⇒ cos((A-C)/2) – cos((A+C)/2) = cos((A+C)/2)
⇒ 2sin(A/2)sin(C/2) = sin(B/2)
⇒ 2{√(s-b)(s-c)√bc} × {√(s-a)(s-b)√ab} = √(s-a)(s-c)√ac
⇒ 2(s – b) = b
⇒ a + b + c – 2b = b
⇒ a + c – b = b
⇒ a + c = 2b

---

Question 4.
The value of cos 5π is
(a) 0
(b) 1
(c) -1
(d) None of these

Answer

Answer: (c) -1
Hint:
Given, cos 5π = cos (π + 4π) = cos π = -1

---

Question 5.
In a triangle ABC, cosec A (sin B cos C + cos B sin C) equals
(a) none of these
(b) c/a
(c) 1
(d) a/c

Answer

Answer: (c) 1
Hint:
Given cosec A (sin B cos C + cos B sin C)
= cosec A × sin(B+C)
= cosec A × sin(180 – A)
= cosec A × sin A
= cosec A × 1/cosec A
= 1

---

Question 6.
If the angles of a triangle be in the ratio 1 : 4 : 5, then the ratio of the greatest side to the smallest side is
(a) 4 : (√5 – 1)
(b) 5 : 4
(c) (√5 – 1) : 4
(d) none of these

Answer

Answer: (a) 4 : (√5 – 1)
Hint:
Given, the angles of a triangle be in the ratio 1 : 4 : 5
⇒ x + 4x + 5x = 180
⇒ 10x = 180
⇒ x = 180/10
⇒ x = 18
So, the angle are: 18, 72, 90
Since a : b : c = sin A : sin B : sin C
⇒ a : b : c = sin 18 : sin 72 : sin 90
⇒ a : b : c = (√5 – 1)/4 : {√(10 + 2√5)}/4 : 1
⇒ a : b : c = (√5 – 1) : {√(10 + 2√5)} : 4
Now, c /a = 4/(√5 – 1)
⇒ c : a = 4 : (√5 – 1)

---

Question 7.
The value of cos 180° is
(a) 0
(b) 1
(c) -1
(d) infinite

Answer

Answer: (c) -1
Hint:
180 is a standard degree generally we all know their values but if we want to go theoretically then
cos(90 + x) = – sin(x)
So, cos 180 = cos(90 + 90)
= -sin 90
= -1 {sin 90 = 1}
So, cos 180 = -1

---

Question 8.
The perimeter of a triangle ABC is 6 times the arithmetic mean of the sines of its angles. If the side b is 2, then the angle B is
(a) 30°
(b) 90°
(c) 60°
(d) 120°

Answer

Answer: (b) 90°
Hint:
Let the lengths of the sides if ∆ABC be a, b and c
Perimeter of the triangle = 2s = a + b + c = 6(sinA + sinB + sinC)/3
⇒ (sinA + sinB + sinC) = ( a + b + c)/2
⇒ (sinA + sinB + sinC)/( a + b + c) = 1/2
From sin formula,Using
sinA/a = sinB/b = sinC/c = (sinA + sinB + sinC)/(a + b + c) = 1/2
Now, sinB/b = 1/2
Given b = 2
So, sinB/2 = 1/2
⇒ sinB = 1
⇒ B = π/2

---

Question 9:
If 3 × tan(x – 15) = tan(x + 15), then the value of x is
(a) 30
(b) 45
(c) 60
(d) 90

Answer

Answer: (b) 45
Hint:
Given, 3×tan(x – 15) = tan(x + 15)
⇒ tan(x + 15)/tan(x – 15) = 3/1
⇒ {tan(x + 15) + tan(x – 15)}/{tan(x + 15) – tan(x – 15)} = (3 + 1)/(3 – 1)
⇒ {tan(x + 15) + tan(x – 15)}/{tan(x + 15) – tan(x – 15)} = 4/2
⇒ {tan(x + 15) + tan(x – 15)}/{tan(x + 15) – tan(x – 15)} = 2
⇒ sin(x + 15 + x – 15)/sin(x + 15 – x + 15) = 2
⇒ sin 2x/sin 30 = 2
⇒ sin 2x/(1/2) = 2
⇒ 2 × sin 2x = 2
⇒ sin 2x = 1
⇒ sin 2x = sin 90
⇒ 2x = 90
⇒ x = 45

---

Question 10.
If the sides of a triangle are 13, 7, 8 the greatest angle of the triangle is
(a) π/3
(b) π/2
(c) 2π/3
(d) 3π/2

Answer

Answer: (c) 2π/3
Hint:
Given, the sides of a triangle are 13, 7, 8
Since greatest side has greatest angle,
Now Cos A = (b² + c² – a²)/2bc
⇒ Cos A = (7² + 8² – 13²)/(2×7×8)
⇒ Cos A = (49 + 64 – 169)/(2×7×8)
⇒ Cos A = (113 – 169)/(2×7×8)
⇒ Cos A = -56/(2×56)
⇒ Cos A = -1/2
⇒ Cos A = Cos 2π/3
⇒ A = 2π/3
So, the greatest angle is
= 2π/3

---

Question 11.
The value of tan 20 × tan 40 × tan 80 is
(a) tan 30
(b) tan 60
(c) 2 tan 30
(d) 2 tan 60

Answer

Answer: (b) tan 60
Hint:
Given, tan 20 × tan 40 × tan 80
= tan 40 × tan 80 × tan 20
= [{sin 40 × sin 80}/{cos 40 × cos 80}] × (sin 20/cos 20)
= [{2 * sin 40 × sin 80}/{2 × cos 40 × cos 80}] × (sin 20/cos 20)
= [{cos 40 – cos 120}/{cos 120 + cos 40}] × (sin 20/cos 20)
= [{cos 40 – cos (90 + 30)}/{cos (90 + 30) + cos 40}] × (sin 20/cos 20)
= [{cos 40 + sin30}/{-sin30 + cos 40}] × (sin 20/cos 20)
= [{(2 × cos 40 + 1)/2}/{(-1 + cos 40)/2}] × (sin 20/cos 20)
= [{2 × cos 40 + 1}/{-1 + cos 40}] × (sin 20/cos 20)
= [{2 × cos 40 × sin 20 + sin 20}/{-cos 20 + cos 40 × cos 20}]
= (sin 60 – sin 20 + sin 20)/(-cos 20 + cos 60 + cos 20)
= sin 60/cos 60
= tan 60
So, tan 20 × tan 40 × tan 80 = tan 60

---

Question 12.
If the angles of a triangle be in the ratio 1 : 4 : 5, then the ratio of the greatest side to the smallest side is
(a) 4 : (√5 – 1)
(b) 5 : 4
(c) (√5 – 1) : 4
(d) none of these

Answer

Answer: (a) 4 : (√5 – 1)
Hint:
Given, the angles of a triangle be in the ratio 1 : 4 : 5
⇒ x + 4x + 5x = 180
⇒ 10x = 180
⇒ x = 180/10
⇒ x = 18
So, the angle are: 18, 72, 90
Since a : b : c = sin A : sin B : sin C
⇒ a : b : c = sin 18 : sin 72 : sin 90
⇒ a : b : c = (√5 – 1)/4 : {√(10 + 2√5)}/4 : 1
⇒ a : b : c = (√5 – 1) : {√(10 + 2√5)} : 4
Now, c /a = 4/(√5 – 1)
⇒ c : a = 4 : (√5 – 1)

---

Question 13.
The general solution of √3 cos x – sin x = 1 is
(a) x = n × π + (-1)n × (π/6)
(b) x = π/3 – n × π + (-1)n × (π/6)
(c) x = π/3 + n × π + (-1)n × (π/6)
(d) x = π/3 – n × π + (π/6)

Answer

Answer: (c) x = π/3 + n × π + (-1)n × (π/6)
Hint:
√3 cos x-sin x=1
⇒ (√3/2)cos x – (1/2)sin x = 1/2
⇒ sin 60 × cos x – cos 60 × sin x = 1/2
⇒ sin (x – 60) = 1/2
⇒ sin (x – π/3) = sin 30
⇒ sin (x – π/3) = sinπ/6
⇒ x – π/3 = n × π + (-1)n × (π/6) {where n ∈ Z}
⇒ x = π/3 + n × π + (-1)n × (π/6)

---

Question 14.
If tan² θ = 1 – e², then the value of sec θ + tan³ θ × cosec θ is
(a) 2 – e²
(b) (2 – e²)1/2
(c) (2 – e²)²
(d) (2 – e²)3/2

Answer

Answer: (d) (2 – e²)3/2
Hint:
Given, tan² θ = 1 – e²
⇒ tan θ = √(1 – e²)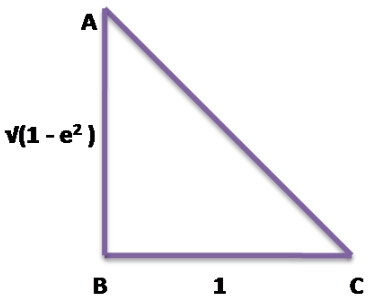

From the figure and Pythagorus theorem,
AC² = AB² + BC²
⇒ AC² = {√(1 – e²)}² + 12
⇒ AC² = 1 – e² + 1
⇒ AC² = 2 – e²
⇒ AC = √(2 – e²)
Now, sec θ = √(2 – e²)
cosec θ = √(2 – e²)/√(1 – e²)
and tan θ = √(1 – e²)
Given, sec θ + tan³ θ × cosec θ
= √(2 – e²) + {(1 – e²)3/2 × √(2 – e²)/√(1 – e²)}
= √(2 – e²) + {(1 – e²) × (1 – e²) × √(2 – e²)/√(1 – e²)}
= √(2 – e²) + (1 – e²) × √(2 – e²)
= √(2 – e²) × (1 + 1 – e²)
= √(2 – e²) × (2 – e²)
= (2 – e²)3/2
So, sec θ + tan³ θ × cosec θ = (2 – e²)3/2

---

Question 15.
The value of cos 20 + 2sin² 55 – √2 sin65 is
(a) 0
(b) 1
(c) -1
(d) None of these

Answer

Answer: (b) 1
Hint:
Given, cos 20 + 2sin² 55 – √2 sin65
= cos 20 + 1 – cos 110 – √2 sin65 {since cos 2x = 1 – 2sin² x}
= 1 + cos 20 – cos 110 – √2 sin65
= 1 – 2 × sin {(20 + 110)/2 × sin{(20 – 110)/2} – √2 sin65 {Apply cos C – cos D formula}
= 1 – 2 × sin 65 × sin (-45) – √2 sin65
= 1 + 2 × sin 65 × sin 45 – √2 sin65
= 1 + (2 × sin 65)/√2 – √2 sin65
= 1 + √2 ( sin 65 – √2 sin 65
= 1
So, cos 20 + 2sin² 55 – √2 sin65 = 1

---

Question 16.
If the radius of the circumcircle of an isosceles triangle PQR is equal to PQ ( = PR), then the angle P is
(a) 2π/3
(b) π/3
(c) π/2
(d) π/6

Answer

Answer: (a) 2π/3
Hint:
Let S be the center of the circumcircle of triangle PQR.
So, SP = SQ = SR = PQ = PR, where SP, SQ & SR are radii.
Thus SPQ & SPR are equilateral triangles.
⇒ ∠QSP = 60°;
Similarly ∠RQP = 60°
⇒ Angle at the center QSP = 120°
So, SRPQ is a rhombus, since all the four sides are equal.
Hence, its opposite angles are equal; so ∠P = ∠QSP = 120°

---

Question 17.
If cos a + 2cos b + cos c = 2 then a, b, c are in
(a) 2b = a + c
(b) b² = a × c
(c) a = b = c
(d) None of these

Answer

Answer: (a) 2b = a + c
Hint:
Given, cos A + 2 cos B + cos C = 2
⇒ cos A + cos C = 2(1 – cos B)
⇒ 2 cos((A + C)/2) × cos((A-C)/2 = 4 sin² (B/2)
⇒ 2 sin(B/2)cos((A-C)/2) = 4sin² (B/2)
⇒ cos((A-C)/2) = 2sin (B/2)
⇒ cos((A-C)/2) = 2cos((A+C)/2)
⇒ cos((A-C)/2) – cos((A+C)/2) = cos((A+C)/2)
⇒ 2sin(A/2)sin(C/2) = sin(B/2)
⇒ 2{√(s-b)(s-c)√bc} × {√(s-a)(s-b)√ab} = √(s-a)(s-c)√ac
⇒ 2(s – b) = b
⇒ a + b + c – 2b = b
⇒ a + c – b = b
⇒ a + c = 2b

---

Question 18.
The value of 4 × sin x × sin(x + π/3) × sin(x + 2π/3) is
(a) sin x
(b) sin 2x
(c) sin 3x
(d) sin 4x

Answer

Answer: (c) sin 3x
Hint:
Given, 4 × sin x × sin(x + π/3) × sin(x + 2π/3)
= 4 × sin x × {sin x × cos π/3 + cos x × sin π/3} × {sin x × cos 2π/3 + cos x × sin 2π/3}
= 4 × sin x × {(sin x)/2 + (√3 × cos x)/2} × {-(sin x)/2 + (√3 × cos x)/2}
= 4 × sin x × {-(sin 2x)/4 + (3 × cos 2x)/4}
= sin x × {-sin 2x + 3 × cos 2x}
= sin x × {-sin 2x + 3 × (1 – sin 2x)}
= sin x × {-sin 2x + 3 – 3 × sin 2x}
= sin x × {3 – 4 × sin 2x}
= 3 × sin x – 4 sin 3x
= sin 3x
So, 4 × sin x × sin(x + π/3) × sin(x + 2π/3) = sin 3x

---

Question 19.
If tan A – tan B = x and cot B – cot A = y, then the value of cot (A – B) is
(a) x + y
(b) 1/x + y
(c) x + 1/y
(d) 1/x + 1/y

Answer

Answer: (d) 1/x + 1/y
Hint:
Given,
tan A – tan B = x ……………. 1
and cot B – cot A = y ……………. 2
From equation,
1/cot A – 1/cot B = x
⇒ (cot B – cot A)/(cot A × cot B) = x
⇒ y/(cot A × cot B) = x {from equation 2}
⇒ y = x × (cot A × cot B)
⇒ cot A × cot B = y/x
Now, cot (A – B) = (cot A × cot B + 1)/(cot B – cot A)
⇒ cot (A – B) = (y/x + 1)/y
⇒ cot (A – B) = (y/x) × (1/y) + 1/y
⇒ cot (A – B) = 1/x + 1/y

---

Question 20.
The value of (sin 7x + sin 5x) /(cos 7x + cos 5x) + (sin 9x + sin 3x) / (cos 9x + cos 3x) is
(a) tan 6x
(b) 2 tan 6x
(c) 3 tan 6x
(d) 4 tan 6x

Answer

Answer: (b) 2 tan 6x
Hint:
Given, (sin 7x + sin 5x) /(cos 7x + cos 5x) + (sin 9x + sin 3x) / (cos 9x + cos 3x)
⇒ [{2 × sin(7x+5x)/2 × cos(7x-5x)/2}/{2 × cos(7x+5x)/2 × cos(7x-5x)/2}] + [{2 × sin(9x+3x)/2 × cos(9x-3x)/2}/{2 × cos(9x+3x)/2 × cos(9x-3x)/2}]
⇒ [{2 × sin 6x × cosx}/{2 × cos 6x × cosx}] + [{2 × sin 6x × cosx}/{2 × cos 6x × cosx}]
⇒ (sin 6x/cos 6x) + (sin 6x/cos 6x)
⇒ tan 6x + tan 6x
⇒ 2 tan 6x

---