NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4
Unless stated otherwise, take π =
Question 1.
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular .ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:
Given: upper diameter = 4 cm ⇒ upper radius =
lower diameter = 2 cm ⇒ lower radius =
height of glass = 14 cm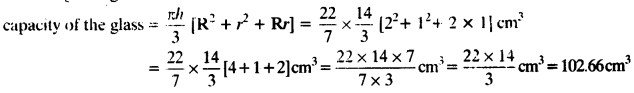
Question 2.
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Solution:
Given: upper circumference of the frustum = 18 cm
Slant height (l) = 4 cm
We have C.S.A of the frustum = π (r1 + r2)l
Putting values from equation (i) and (ii), we get
Curved surface area = (πr1 + πr2)l = (9 + 3) x 4 = 12 x 4 = 48 cm²
Question 3.
A fez, the cap used by the Turks, is shaped like the frustum of a cone (see figure). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.
Solution:
Radius of open side (r1) = 10 cm
Radius of upper base (r2) = 4 cm
Slant height (l) = 15 cm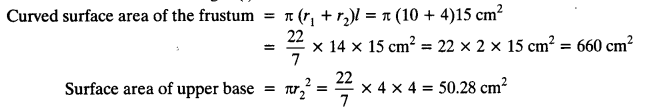
Total surface area of the cap = C.S.A. of the frustum + Area of upper base
= 660 cm² + 50.28 cm² = 710.28 cm²
Question 4.
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 8 per 100 cm2. (Take π = 3.14)
Solution:
Radius of the lower end (r1) = 8 cm
Radius of the upper end (r2) = 20 cm
Height of the frustum (h) = 16 cm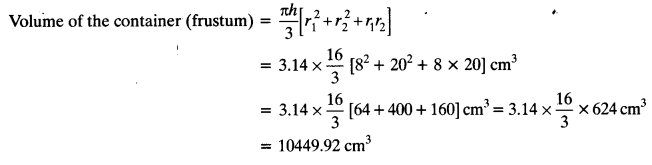

Question 5.
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter
Solution:
Let ADC is a cone with vertical angle 600.
Now, cone is cut into two parts, parallel to its base at height 10 cm.
Radius of larger end of the frustum = R1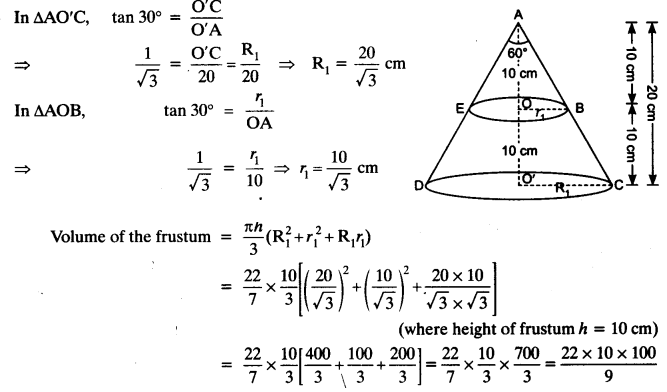
A wire be formed having diameter
Volume of wire so obtained = πr²H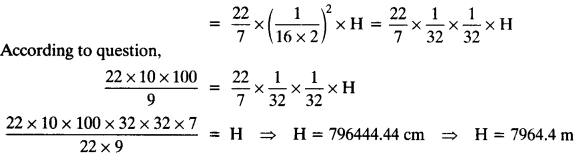








0 Comments