NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3

  

NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3

Ex 4.3 Class 10 Maths Question 1.
Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x2 – 7x + 3 = 0
(ii) 2x2 + x – 4 = 0
(iii) 4x2 + 4√3x + 3 = 0
(iv) 2x2 + x + 4 = 0
Solution: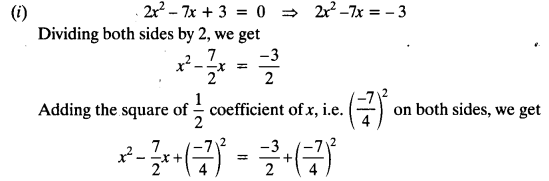

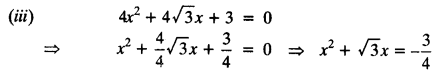
Exercise 4.3 Class 10 Maths Question 2.
Find the roots of the quadratic equations by applying the quadratic formula.
(i) 2x2 – 7x + 3 = 0
(ii) 2x2 – x + 4 = 0
(iii) 4x2 – 4√3x + 3 = 0
(iv) 2x2 – x + 4 = 0
Solution:
(i) 2x2 – 7x + 3 = 0
This is of the form ax2 + bx + c = 0,
where a = 2, b = -7 and c = 3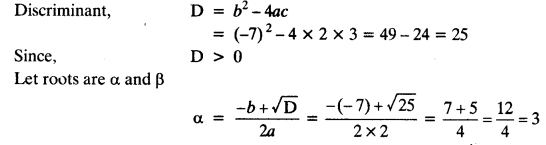

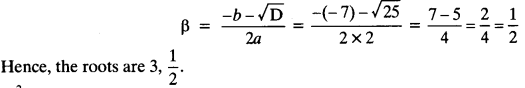
(ii) 2x2 – x + 4 = 0
This is of the form ax2 + bx + c = 0,
where a = 2, b = 1 and c = – 4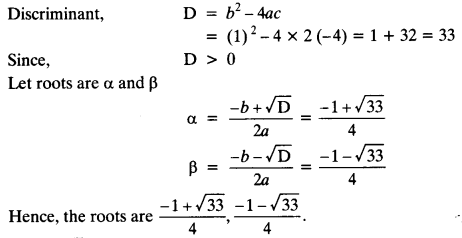

(iii) 4x2 – 4√3x + 3 = 0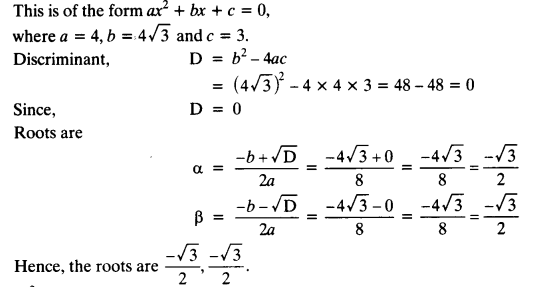

(iv) 2x2 – x + 4 = 0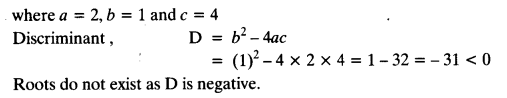

4.3 Class 10 Maths Question 3.
Find the roots of the following equations:


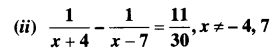
Solution:

Class 10 Maths Chapter 4 Exercise 4.3 Question 4.
The sum of the reciprocals of Rehman’s ages, (in years) 3 years ago and 5 years from now is 13 Find his present age.
Solution:
Let the present age of Rehman be x years
3 years ago Rehman’s age was = (x – 3) years
5 years from now Rehman’s age will be = (x + 5) years

Class 10 Ex 4.3 Maths Quadratic Equations Question 5.
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
Solution:
Let the marks secured by Shefali in Mathematics = x Then,
According to question,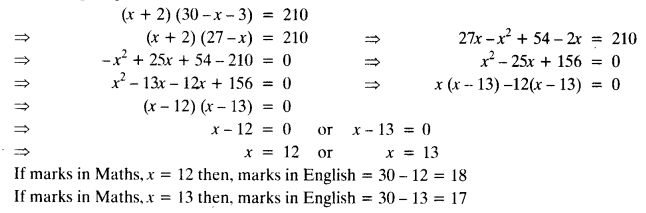

4.3 Maths Class 10 Chapter 4 Question 6.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution:
Let the shorter side of rectangle = x m
Then, longer side = (x + 30) m and diagonal = (x + 60) m
In ΔABC, (x + 60)2 = (x + 30)2 + (x)2 [Pythagoras Theorem]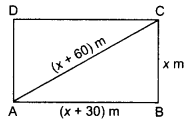

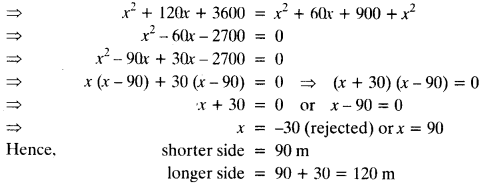
Ex4.3 Class 10 Maths Question 7.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Solution:
Let the smaller number = x
and the larger number = y
According to question,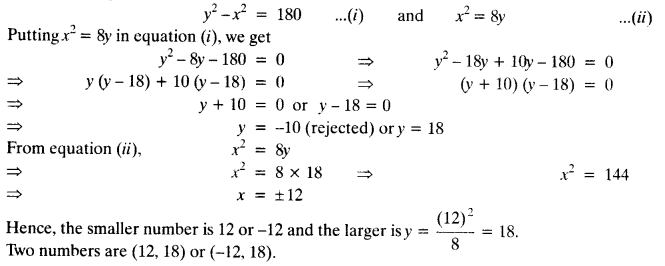

Ex 4.3 Chapter 4 Maths Question 8.
A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
Total distance travelled = 360 km
Let uniform speed be x km/h
Then, increased speed = (x + 5) km/h
According to question,

Exercise 4.3 Class 10 Maths Question 9.
Two water taps together can fill a tank in 938 hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution:
Let larger pipe fills the tank in x hours and the smaller pipe fills the tank in y hours.
The tank filled by the larger pipe in 1 hour = 1x

Ncert Solutions For Class 10 Maths Chapter 4 Exercise 4.3 Question 10.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bengaluru (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
Solution:
Let the speed of passenger train = x km/h
Then, the speed of express train be (x + 11) km/h
According to question,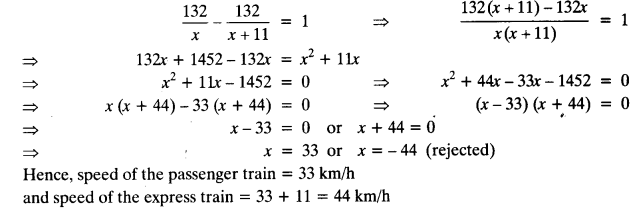

Exercise 4.3 Class 10th Question 11.
Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.
Solution:
Let the sides of two squares be x m and y m
According to question,