Integrals Class 12 Maths Important Questions Chapter 7

 

Integrals Class 12 Important Questions with Solutions Previous Year Questions

Question 1.
Find ∫sin2x−cos2x dx. (All India 2017)
Answer: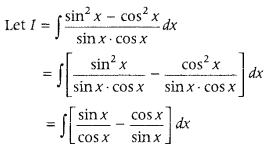

= ∫(tan x – cot x) dx
= ∫ tan x dx – ∫ cot x dx
= log |sec x| – [- log|cosec x|] + C
= log |sec x| + log|cosec x| + C
= log |sec x ∙ cosec x| + C

Question 2.
Find ∫sin2x−cos2x dx. (Delhi 2014C)
Answer: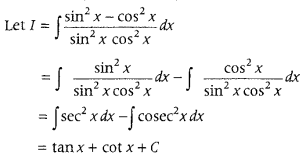

Question 3.
Find ∫sin6x dx. (All India 2014C)
Answer: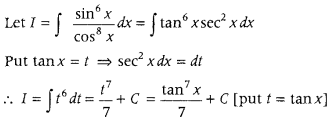

Question 4.
Evaluate ∫sin2xcos2x. (Delhi 2014C; Foreign 2014)
Answer:
Let I = ∫sin2xcos2x
= ∫(sin2x+cos2x) [∵ sin2θ + cos2θ = 1]
= ∫(sec2x + cosec2x) dx
= ∫sec2 xdx + ∫ cosec2x dx
= tan x – cot x + C

Alternate Method:
On dividing the numerator and denominator by cos4 x, we get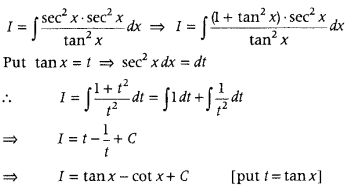

Question 5.
Evaluate ∫cos-1(sin x) dx. (Delhi 2014C)
Answer: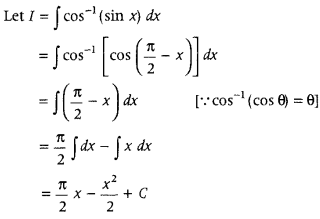

Question 6.
Write the anti-derivative of (3√x + 1x√ (Delhi 2014)
Answer: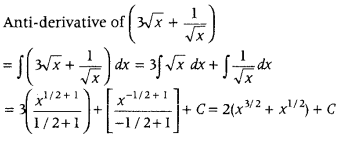

Question 7.
Evaluate ∫(1 – x)√x dx. (Delhi 2012)
Answer:
First, multiply the two functions and then use
∫xn dx = xn+1n+1 + C, n ≠ – 1.

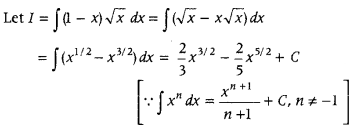
Question 8.
Given, ∫ex (tan x + 1) sec x dx = ex f(x) + C.
Write f(x) satisfying above. (All India 2012; Foregin 2011)
Answer:
Use the relation ∫ex [f(x) + f'(x)dx = ex f(x) + C and simplify it.

Given that ∫ex (tan x + 1) sec x dx = ex ∙ f(x) + C
⇒ ∫ ex (sec x + sec x tan x)dx = ex f(x) + C
⇒ ex . sec x + C = ex f(x) + C
[∵ ex {f(x) + f’(x)}dx = ex f(x) + C and here ddx (sec x) = sec x tan x]
On comparing both sides, we get
f(x) = sec x

Question 9.
Evaluate ∫1+cos2x dx. (Foreign 2012)
Answer: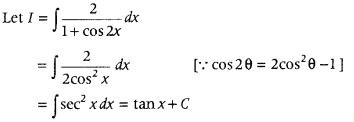

Question 10.
Write the value of ∫x+cos6x dx. (All India 2012C)
Answer: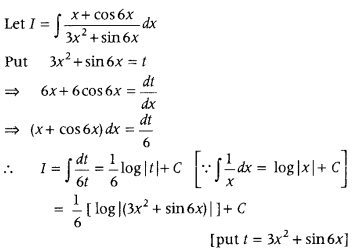

Question 11.
Write the value of ∫sec2x dx. (Delhi 2012C, 2011)
Answer: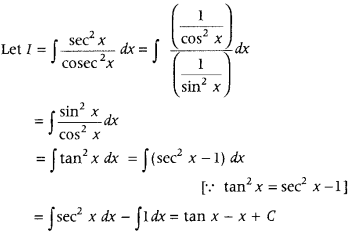

Question 12.
Write the value of ∫dxx2+16 (Delhi 2011)
Answer: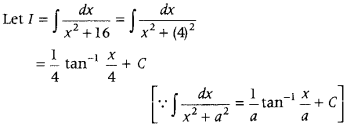

Question 13.
Write the value of ∫2−3sinx dx. (Delhi 2011)
Answer:
Let I = ∫2−3sinx dx
= ∫(2cos2x−3sinxcos2x) dx
= ∫(2 sec2 x – 3 sec x tan x) dx
= 2∫sec2x dx – 3∫sec x tan x dx
= 2 tan x – 3 sec x + C

Question 14.
Write the value of ∫ sec x(sec x + tan x)dx. (Delhi 2011)
Answer:
Let I = ∫sec x(sec x + tan x)dx
= ∫(sec2x + sec x tan x)dx
= ∫sec2 x dx + ∫sec x tan x dx
= tan x + sec x + C

Question 15.
Evaluate ∫dx1−x2√ (All India 2011)
Answer: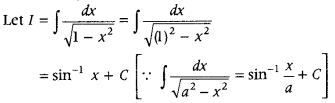

Question 16.
Evaluate ∫(logx)2 dx. (All India 2011)
Answer: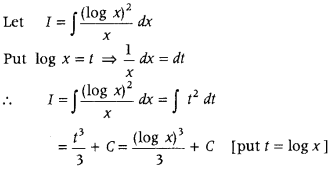

Question 17.
Evaluate ∫ tan−1x dx. (All India 2011)
Answer: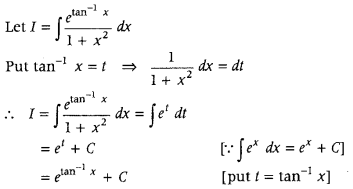

Question 18.
Evaluate ∫ (ax + b )3 dx. (All India 2011)
Answer: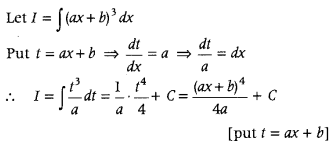

Question 19.
Evaluate ∫(1+logx)2 dx. (ForeIgn 2011; Delhi 2009)
Answer: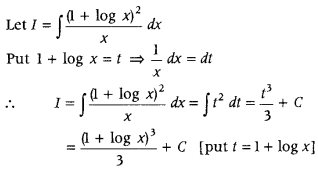

Question 20.
Evaluate ∫e2x−e−2xe2x+e−2x (Foreign 2011)
Answer: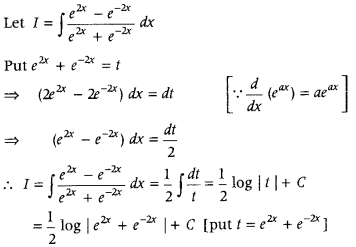

Question 21.
Evaluate ∫cosx√ dx. (Foreign 2011)
Answer: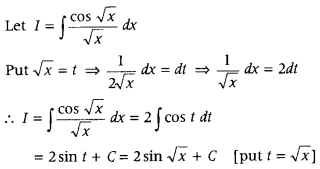

Question 22.
Evaluate ∫2cosx (All India 2011C)
Answer:

Question 23.
Evaluate ∫x3−x2+x−1x−1 (Delhi 2011C)
Answer:
First, factorise numerator and cancel out common factor from numerator and denominator and then integrate.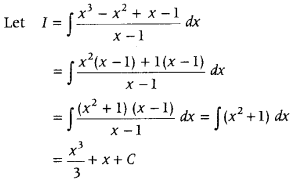

Question 24.
Write the value of ∫1−sinxdx. (All India 2011C)
Answer:
Let I = ∫1−sinx dx
= ∫(1cos2x−sinxcos2x) dx
= ∫ sec2x dx – ∫ sec x tan x dx
= tan x – sec x + C

Question 25.
Evaluate ∫2cosx dx. (All IndIa 2011C, 2009, 2008)
Answer:
– 2 cosec x + C

Question 26.
Evaluate ∫x3−1x2 dx. (Delhi 2010C)
Answer: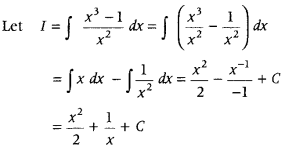

Question 27.
Evaluate ∫sec2 (7 – 4x) dx. (Delhi 2010; All India 2010)
Answer: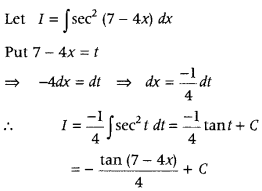

Question 28.
Evaluate ∫logx dx. (All lndia 2010C)
Answer:
(logx)2 + C

Question 29.
Evaluate ∫ 2x dx. (All India 2010C)
Answer:
Let I = ∫ 2x dx = log2 + C
[∵ ∫ax dx = loga + C]

Question 30.
Find ∫sec2x dx. (Delhi 2019)
Answer: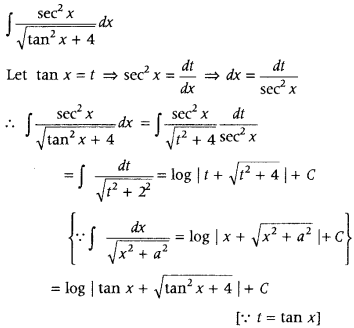

Question 31.
Find: ∫ 1−sin2x dx, π4 < x < π2. (Delhi 2019)
Answer: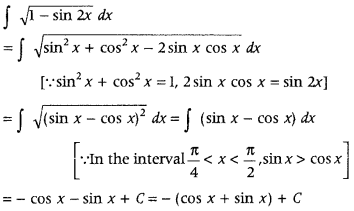

Question 32.
Find: ∫ sin-1 (2x) dx. (Delhi 2019)
Answer:

Question 33.
Find the values of ∫tan2x⋅sec2x dx. (Delhi 2019)
Answer: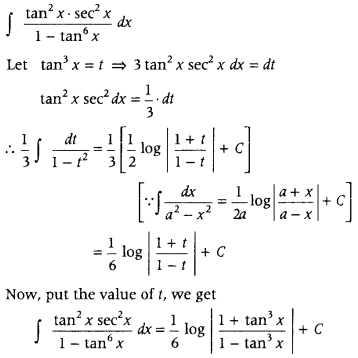

Question 34.
Find the value of ∫ sin x ∙ log cos x dx. (Delhi 2019)
Answer:
∫ sin x ∙ log cos x dx
Put cos x = t ⇒ – sin x dx = dt
∴ – ∫ log t dt ⇒ – ∫ (log t) ∙ 1 dt
⇒ [log t ∫ 1 dt – ∫ {ddt (log t) ∫ 1 dt} dt]
⇒ [(log t) ∙ t – ∫ 1t ∙ t dt]
⇒ – [t ∙ log t – ∫ 1 dt]
⇒ – [t log t – t] + C
⇒ – t ∙ log 1 + 1 + C
⇒ cos x log cos x + cos x + C

Question 35.
Find ∫ 3−2x−x2−−−−−−−−−√ dx. (All India 2019)
Answer: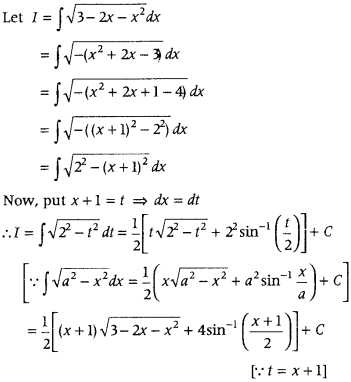

Question 36.
Find ∫sin3x+cos3x dx. (All India 2019)
Answer: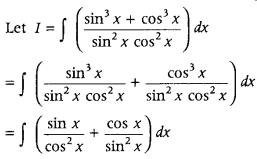

= ∫ [(tan x ∙ sec x ) + (cot x ∙ cosec x)] dx
= ∫ sec x ∙ tan x dx + ∫ cot x ∙ cosec x dx
= sec x + (- cosec x) + C = sec x – cosec x + C

Question 37.
Find ∫x−3(x−1)3 ex dx (All India 2019)
Answer: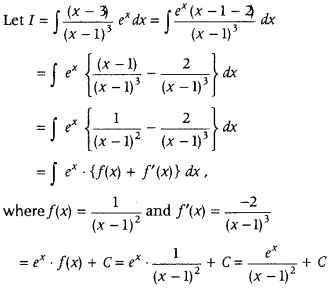

Question 38.
Find ∫x−5(x−3)3 ex dx. (All India 2019)
Answer: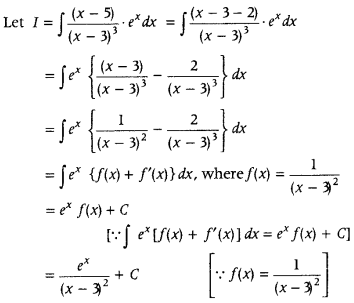

Question 39.
Evaluate ∫cos2x+2sin2x dx (CBSE 2018)
Answer: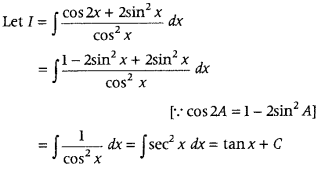

Question 40.
Find: ∫3−5sinx dx (CBSE 2018C)
Answer:
Let I = ∫3−5sinx dx
= ∫(3cos2x−5sinxcos2x) dx
= 3 ∫sec2 x dx – 5 ∫ sec x tan x dx
= 3 tan x – 5 sec x + C

Question 41.
Find ∫dxx2+4x+8 (Delhi 2017)
Answer: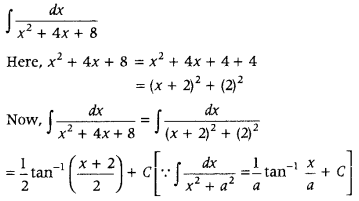

Question 42.
Find ∫dx5−8x−x2 (All India 2017)
Answer: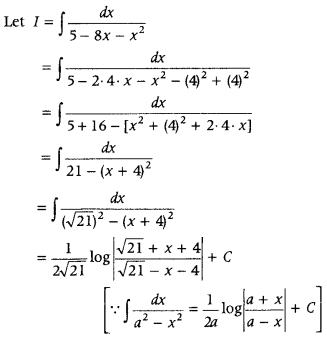

Question 43.
Find: ∫3x+5x2+3x−18 dx. (Delhi 2019)
Answer:
Let I = ∫3x+5x2+3x−18 dx …… (i)
Also, let 3x + 5 = A ddx (x2 + 3x – 18) + B
3x + 5 = A(2x + 3) + B …….. (ii)
On comparing the coefficient of x, we get
2A = 3 ⇒ A = 32
and on comparing the constant term, we gct
B = 5 – 3A ⇒ B = 5 – 3(32) = 12
From Eq. (ii). we get
3x + 5 = 32(2x + 3) + 12 ……. (iii)
From Eqs. (i) and (iii), we get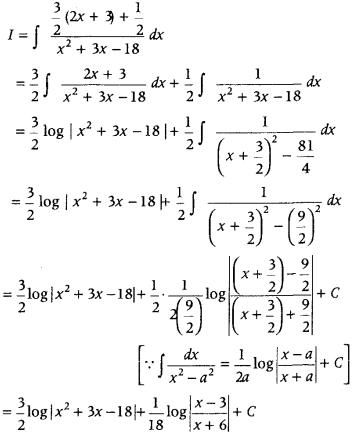

Question 44.
Find the value of ∫cosx dx. (Delhi 2019)
Answer:
Let I = ∫cosx dx
Put sin x = t ⇒ cos x dx = dt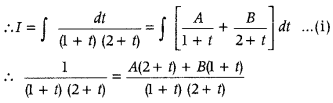

1 = 2A + tA + B + Bt
1 = 1(2A + B) + t(A + B)
On comparing the coefficients of I and constant term on both sides, we get
2A + B = 1 and A + 8 = 0
⇒ A = 1 and B = – 1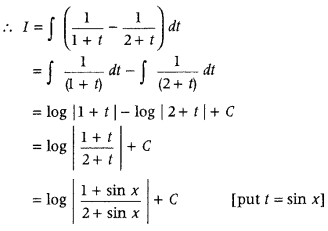

Question 45.
Find ∫x2+x+1(x+2)(x2+1) dx. (All India 2019)
Answer: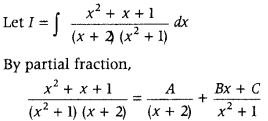

⇒ x2 + x + 1 = A(x2 + 1) + (Bx + C) (x + 2)
Putting x = – 2
4 – 2 + 1 = A(5) + 0 ⇒ 5A = 3 ⇒ A = 35
Putting x = 0,
0 + 0 + 1 = A(0 + 1) + (0 + C) (0 + 2)
⇒ 1 = A + 2C ⇒ 1 = 35 + 2C ⇒ 2C = 25 ⇒ C = 15
and putting x = 1,
⇒ 1 + 1 + 1 = 2A + (8 + C) (3)
⇒ 3 = 2A + 3(B + C)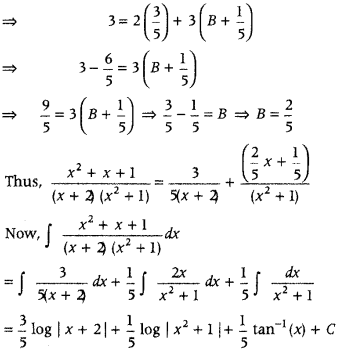

Question 46.
Find ∫2cosx dx. (All India 2019)
Answer: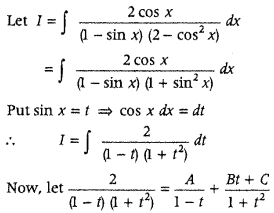

⇒ 2 = A(1 + t2) + (Bt + C) (1 – t)
Putting t = 1 in Eq. (i), we get
2 = 2A ⇒ A = 1
Putting t = 0 in Eq. (1). we get
2 = A + C ⇒ 2 = 1 + C ⇒ C = 1
Putting t = – 1 in Eq. (1), we get
2= 2A + (- B + C)
⇒ 2 = 2 – 2B + 2
⇒ 2B = 2 ⇒ B = 1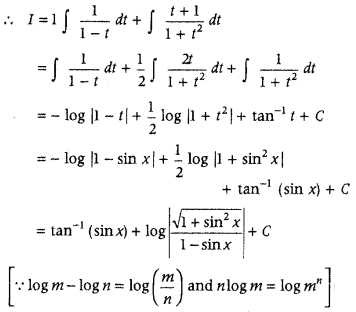

Question 47.
Find ∫2cosx dx. (CBSE 2018)
Answer: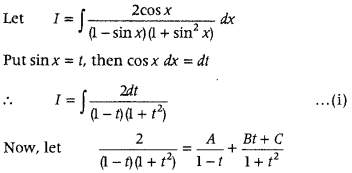

⇒ 2 = (1 + t2)A + (1 – t) (Bt + C)
⇒ 2 = (1 + t2)A + (Bt + C – Bt2 – Ct)
⇒ 2 = t2 (A – B) + t(B – C) + (A + C)
On comparing the coefficients of like powers of t, we get
A – B = 0; B – C = 0 and A + C = 2
⇒ A = B; B = C and A + C = 2
⇒ A = B = C = 1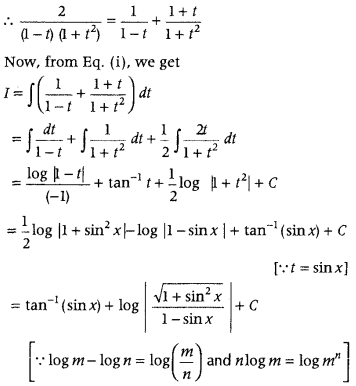

Question 48.
Find ∫4(x−2)(x2+4) dx. (CBSE 2018C)
Answer: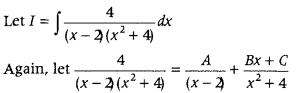

⇒ 4 = A(x2 + 4) + (Bx + C) (x – 2)
⇒ 4 = x2 (A + B) + x(- 2B + C) + 4A – 2C
On equating the coefficients of x2, x and constant form both sides, we get
A + B = 0 ……. (i)
– 2B + C = 0 ……. (ii)
and 4A – 2C = 4 …….. (iii)
On solving Eqs. (i), (ii) and (iii), we get
A = 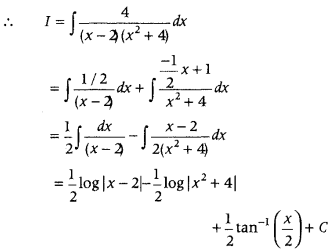12, B = –12 and C = 1

Question 49.
Find ∫2x(x2+1)(x2+2)2 dx. (Delhi 2017)
Answer: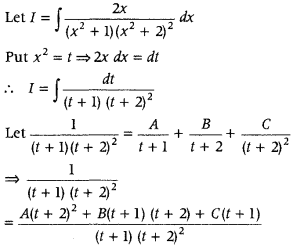

⇒ 1 = A(t + 2)2 + B(t + 1) (t + 2) + C(t + 1)
⇒ 1 = A(t2 + 4 + 4t) + B(t2 + 2t + t + 2) + C(t + 1)
⇒ 1 = A(t2 + 4t + 4) + B(t2 + 3t + 2) + C(t + 1)
⇒ 1 = t2 (A + B) + t(4A + 3B + C) + 4A + 2B + C
On comparing the coefficients of 2, and the constant term from both sides, we get
A + B = 0
4A + 3B + C = 0 ……. (ii)
and 4A + 2B + C = 1 …….. (iii)
From Eq. (1), A = – B
Put the value of A in Eqs. (ii) and (iii), we get
– 4B + 3B + C = 0
⇒ – B + C = 0
⇒ B – C = 0 ……. (iv)
and – 4B + 2B + C = 1
⇒ – 2B + C = 1
⇒ 28 – C = – 1
Now, from Eqs. (iv) and (y), we get
– B = 1 ⇒ B = – 1
∴ A = 1 and C = – 1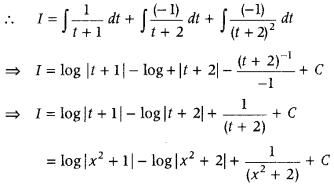

Question 50.
Find ∫2x(x2+1)(x4+4) dx. (Delhi 2017)
Answer: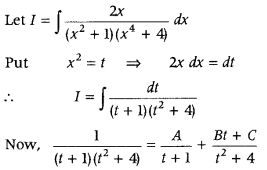

⇒ 1 = A(t2 + 4) + (Bt + C) (t + 1)
⇒ 1 = A(t2 + 4) + (Bt2 + Bt + Ct + C)
⇒ 1 = t2(A + B) +t(B + C) + (4A + C)
On comparing the coefficients of t2, t and constant term from both sides, we get
A + B = 0
B + C = 0 ……… (ii)
4A + C = 1 …….. (iii)
From Eqs. (i) and (ii), we get
A – C = 0 …… (iv)
From Eqs. (iii) and (iv), we get
5A = 1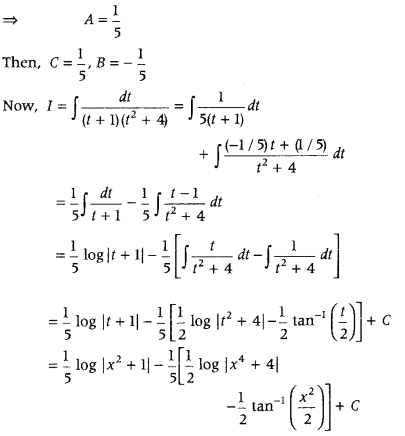

Question 51.
Find ∫cosθ dθ (All India 2017)
Answer:

Question 52.
Find ∫(3sinθ−2)cosθ dθ (Delhi 2016)
Or
Find ∫(3sinx−2)cosx dx.
Answer: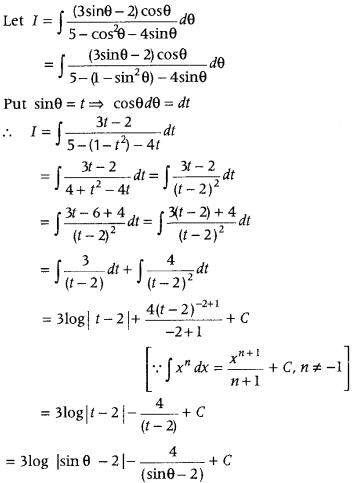

Question 53.
Find ∫x√a3−x3√ dx. (Delhi 2016)
Answer: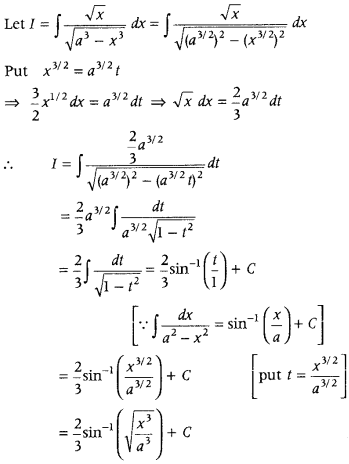

Question 54.
Find ∫(x + 3) (3−4x−x2)−−−−−−−−−−−√ dx. (All India 2016; Delhi 2015, 2014C)
Answer:
First, use the method for integral of the form
∫(px + q)ax2+bx+c−−−−−−−−−−√ dx,
consider (px + q) = Addx (ax2 + bx + c) + B,
simplify and get the values of A and B.
Further, simplify the integrand and use the formula
∫a2−x2−−−−−−√dx = [12xa2−x2−−−−−−√+a22sin−1(xa)+C]
Let I = ∫(x + 3) 3−4x−x2−−−−−−−−−√ dx
Given integral is the form of
∫ (px + q) ax2+bx+c−−−−−−−−−−√ dx
Let (x + 3) = A ddx (3 – 4x – x2) + B
⇒ x + 3 = A(- 4 – 2x) + B
⇒ x + 3 = (- 4A + B) – 2Ax
On comparing the coefficients of x and constant terms, we get
– 2A = I
⇒ A = – 12
and – 4A + B = 3 ⇒ 2 + B = 3 ⇒ B = 1 …….. (1)
Thus. (x + 3) = – 12 (- 4 – 2x) + 1 [from Eq. (1)]
Now, given integral becomes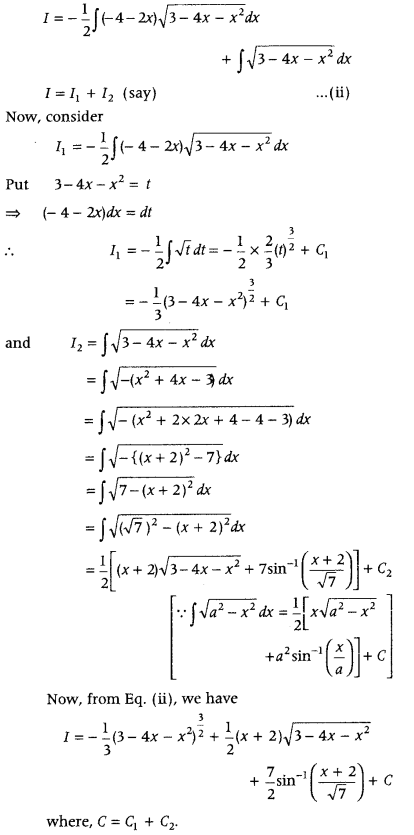

Question 55.
Evaluate ∫x2+x+1(x2+1)(x+2) dx. (All IndIa 2016F 2015, 2009C)
Answer:
First, use the partial traction ¡n the given integrand,
i.e. write = x2+x+1(x2+1)(x+2) = Ax+2 + Bx+Cx2+1
Simplify it and get the values of constants A, B and C.
Further, integrate it to get the result.
Let I = ∫x2+x+1(x2+1)(x+2) dx
By using partial fraction method, we get
x2+x+1(x2+1)(x+2) = Ax+2 + Bx+Cx2+1
⇒ x2 + x + 1 = A(x2 + 1) + (Bx + C) (x + 2)
⇒ x2 + x + 1 = x2 (A + B) + x(2B + C) + (A + 2C)
On comparing the coefficients of x2, x and constant terms both sides, we get
A + B = 1 ……. (ii)
2B + C = 1 …….. (iii)
and A + 2C = 1 ……. (iv)
On substituting the value ofBfrom q. (ii) in Eq. (iii), we get
2(1 – A) + C = 1
⇒ 2 – 2A + C = 1
⇒ 2A – C = 1 ……. (v)

Question 56.
Find ∫(2x−5)e2x(2x−3)3 dx. (All India 2016)
Answer:

Question 57.
Find ∫ (2x + 5) 10−4x−3x2−−−−−−−−−−−√ dx. (Foregin 2016).
Answer: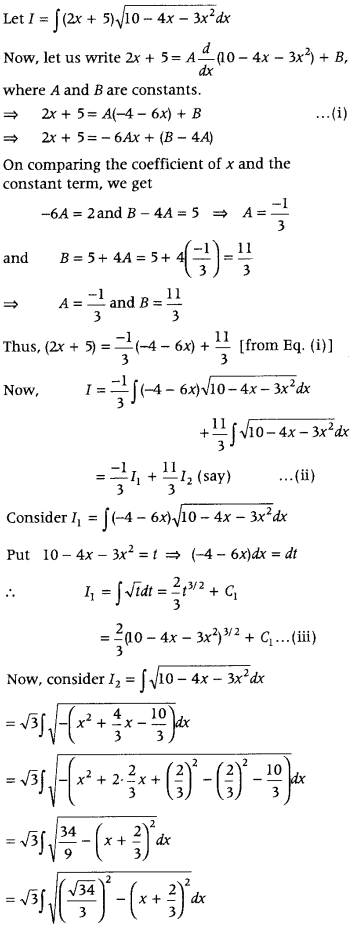

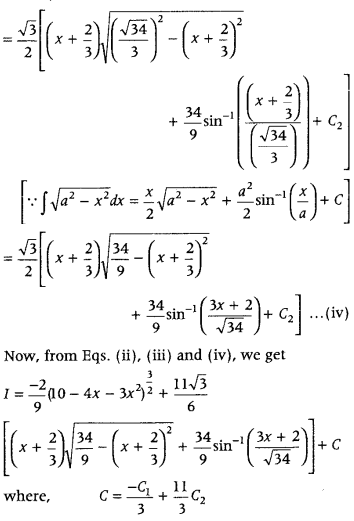
Question 58.
Find ∫(x2+1)(x2+4)(x2+3)(x2−5) (Foregin 2o16)
Answer: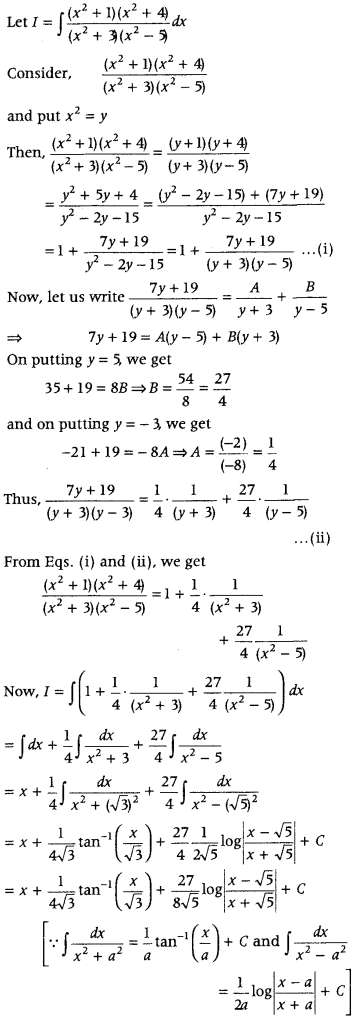

Question 59.
Evaluate ∫xsin−1x dx. (Foreign 2016; Delhi 2012)
Answer:
First, put x = sin t and then use integration by parts and simplify it.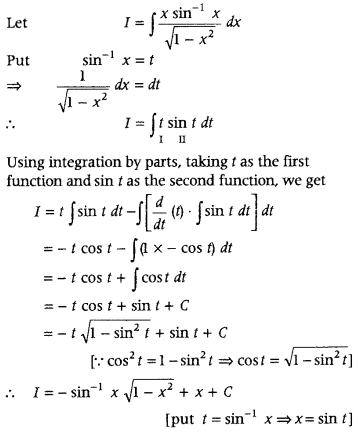

Question 60.
Find ∫sinx+sin2x dx. (Delhi 2015)
Answer:
First, simplify the integrand in such a form that numerator is in sin form and denominator is in cos form, Substitute cos x = t and then convert the given integrand in the form of t.
Now, use partial traction in the integrand and then integrate it. Further, substitute the value oft and get the required result.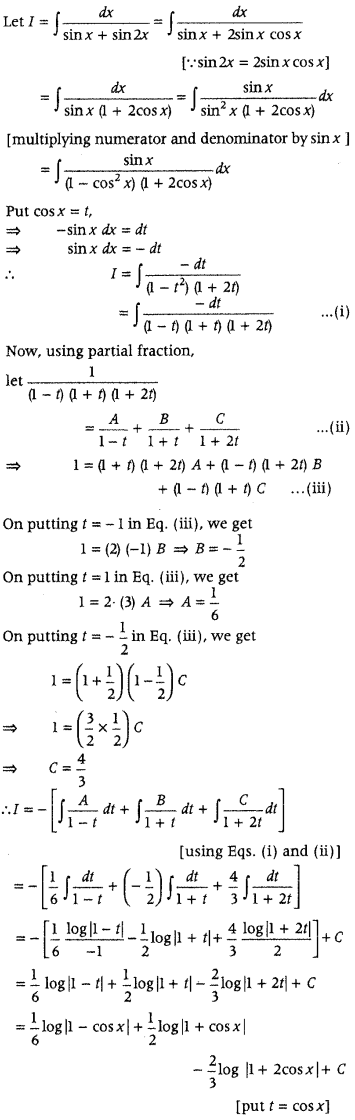

Question 61.
Integrate w.r.t. x, x2−3x+11−x2√ (Delhi 2015)
Answer: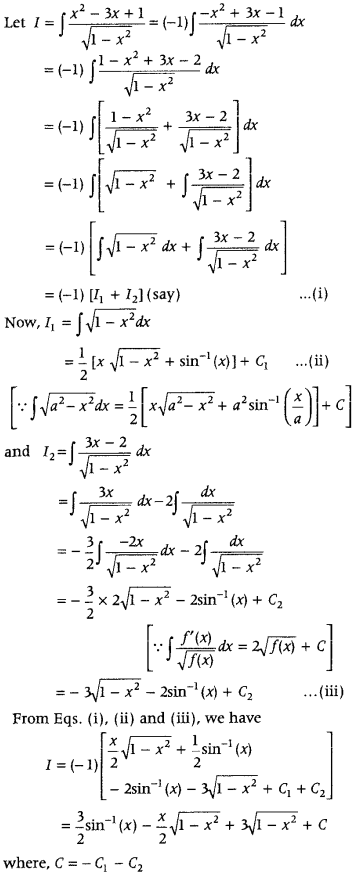

Question 62.
Evaluate ∫(3 – 2x) 2+x−x2−−−−−−−−√ dx. (All India 2015)
Answer:

Question 63.
Find ∫log|x| dx. (All India 2015)
Answer:

Question 64.
Evaluate ∫sin(x−a) dx. (Foreign 2015; Delhi 2013)
Answer:
Let I = ∫sin(x−a) dx
put x + a = t
⇒ dx = dt
∴ I = ∫sin(t−a−a) dt = ∫sin(t−2a) dt
= ∫sintcos2a−costsin2a dt
[∵ sin(A – B) = sin A cos B – cos A sin B]
= ∫ cos 2a dt – ∫sin 2z . cos t dt
= cos 2a [t] – sin 2a log|sin(x + a)| + C1
[put t = x + a]
= x cos 2a – sin 2a log|sin(x + a)| + C
where, C = a cos 2a + C1

Question 65.
∫e2x sin(3x + 1) dx. (Foreign 2015)
Answer: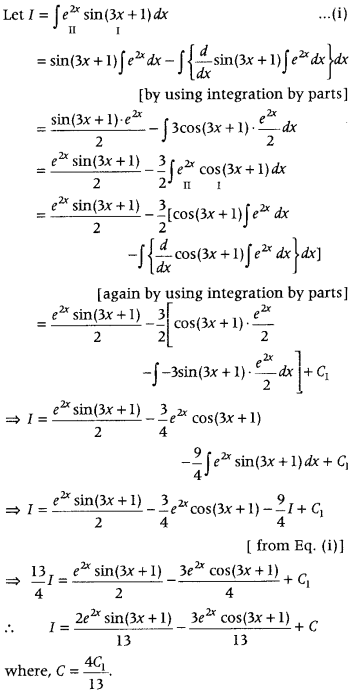

Question 66.
Evaluate ∫x2(x2+4)(x2+9) dx. (Foreign 2015; Delhi 2013)
Answer:

Question 67.
Find ∫(x2+1)ex(x+1)2 dx. (Delhi 2015C)
Answer: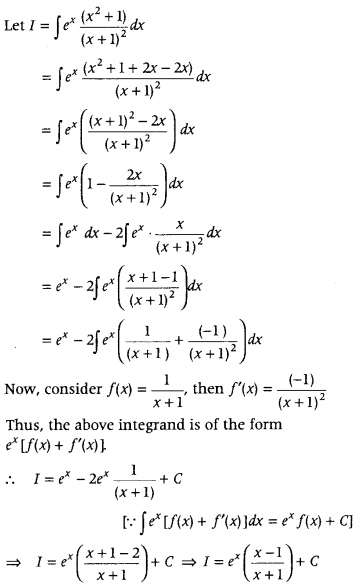

Question 68.
Evaluate ∫ (x – 3) x2+3x−18−−−−−−−−−−√ dx. (Delhi 2014)
Answer:
Here, integrand is of the form (px – q)ax2+bx+c−−−−−−−−−−√, so firstly write x – 3 as x – 3 = Addx (x2 + 3x – 18) + B and find A and B.
Then integrate by using suitable method.

Question 69.
Evaluate ∫x+2x2+5x+6√ (All India 2014)
Answer: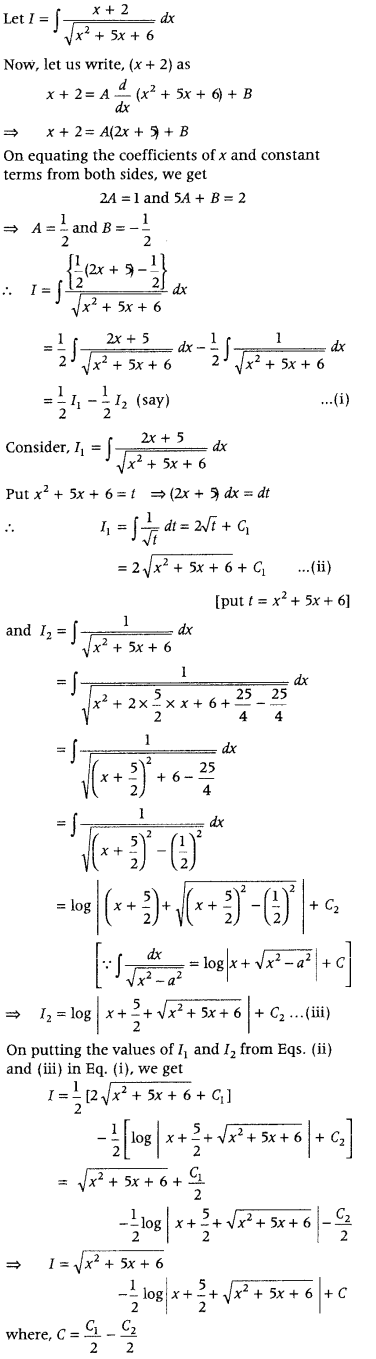

Question 70.
Evaluate ∫ (3x — 2) x2+x+1−−−−−−−−√ dx. (Foreign 2014)
Answer:
I = (x2 + x + 1)3/2 – 78(2x + 1)x2+x+1−−−−−−−−√ – 2116 log∣∣(2x+1)2+x2+x+1−−−−−−−−√∣∣ + C

Question 71.
Find ∫5x−21+2x+3x2 (Delhi 2014C; Delhi 2013)
Answer: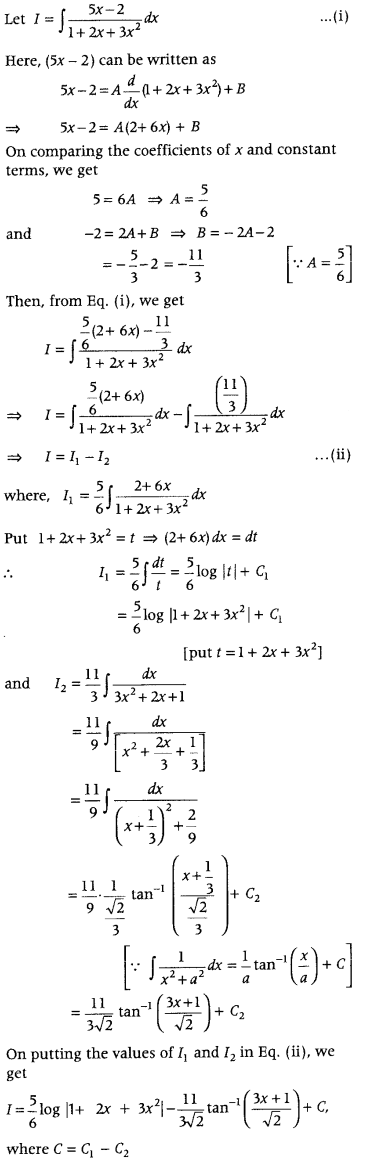

Question 72.
Find ∫x3x4+3x2+2 (All India 2014C)
Answer:
First, put x2 = t and use partial traction to write integrand in simplest form, Then integrate by using suitable formula.

Question 73.
Evaluate ∫xcos−1x dx. (All India 2014C; Foreign 2014)
Answer:
– 1−x2−−−−−√ cos-1 x – x + C

Question 74.
Evaluate ∫sin6x+cos6x dx. (Delhi 2014C)
Answer:
First, use a3 + b3 = (a + b)3 – 3ab(a + b)to write numerator of integrand in simplest form and then integrate by using suitable method.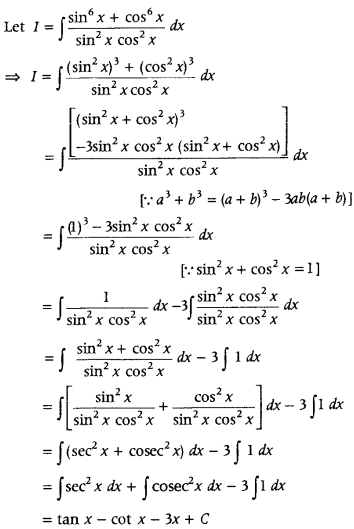

Question 75.
Evaluate ∫e2x (1−sin2x1−cos2x) dx. (Delhi 2013C)
Answer:
First, use trigonometric formulae sin 2θ = 2 sin θ cos θ and cos 2θ = 1 – 2 sin2θ to write integrand in simplest form and then apply integration by parts to integrate.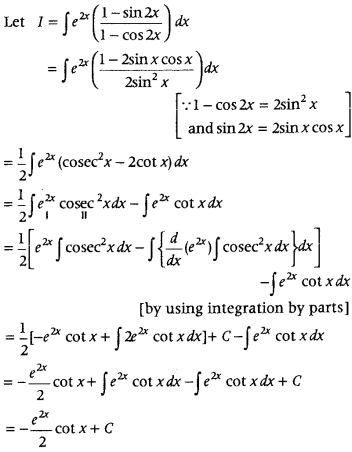

Question 76.
Evaluate ∫3x+1(x+1)2(x+3) dx. (Delhi 2013C)
Answer: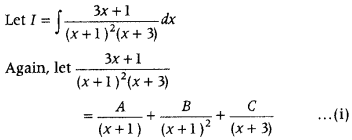

⇒ 3x + 1 = A(x + 1) (x + 3) + B(x + 3)
⇒ 3x + 1 = A(x2 + 4x + 3) + B(x + 3) + C(x2 + 1 + 2x)
⇒ 3x + 1 = (A + C)x2 + (4A + B + 2C)x + 3A + 3B + C
On comparing like powers of x from both sides, we get
A + C = 0
4A + B + 2C = 3
and 3A + 3B + C = 1
On solving, we get A = 2, B = – 1 and C = – 2
∴ Eq. (1) becomes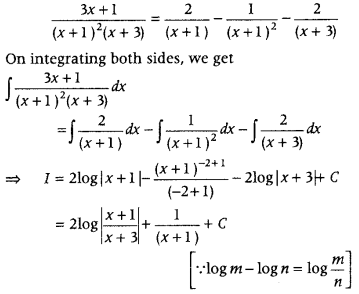

Question 77.
Evaluate ∫2x2+1x2(x2+4) dx. (Delhi 2013)
Answer:

Question 78.
Evaluate ∫x2+1(x2+4)(x2+25) dx. (Delhi 2013)
Answer:
– 114tan-1(x2) + (x5)tan-1 + C

Question 79.
Evaluate ∫cos2x−cos2α dx. (All India 2013)
Answer: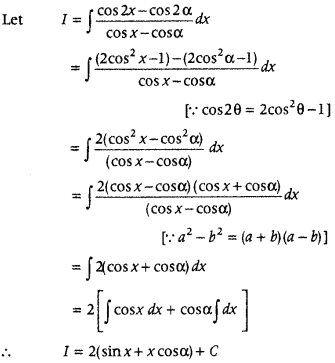

Question 80.
Evaluate ∫x+2x2+2x+3√ (All India 2013)
Answer:
x2+2x+3−−−−−−−−−√ + log|(x + 1) + x2+2x+3−−−−−−−−−√| + C

Question 81.
Evaluate ∫ dxx(x5+3) (All India 2013)
Answer:

Question 82.
Evaluate ∫ dxx(x3+1) (All India 2013)
Answer:
13 log ∣∣x3x3+1∣∣ + C

Question 83.
Evaluate ∫ dxx(x3+8) (All India 2013)
Answer:
18 log ∣∣∣x(x3+8)1/3∣∣∣ + C

Question 84.
Evaluate ∫ 1−sinx√1+cosxe−x2 dx. (All India 2013C)
Answer: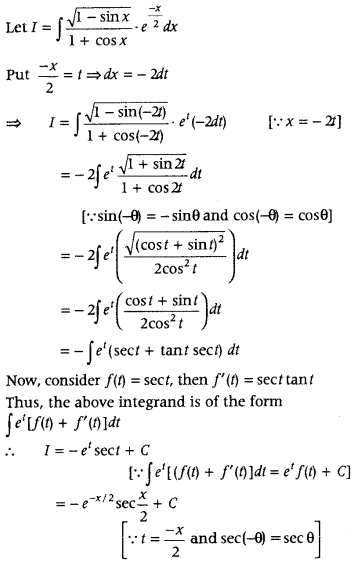

Question 85.
Evaluate ∫ 3x+5x3−x2−x+1 dx. (Delhi 2013C)
Answer:

12 log ∣∣x+1x−1∣∣ – 4x−1 + C

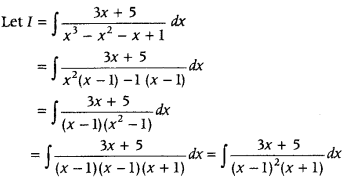
Question 86.
Evaluate ∫ sin x ∙ sin 2x ∙ sin 3x dx. (Delhi 2012)
Answer:
It is a product of three trigonometric functions. So, firstly we take two functions at a time and use the relation 2 sin A sin B = cos(A – B) – cos(A + B) and then integrate it.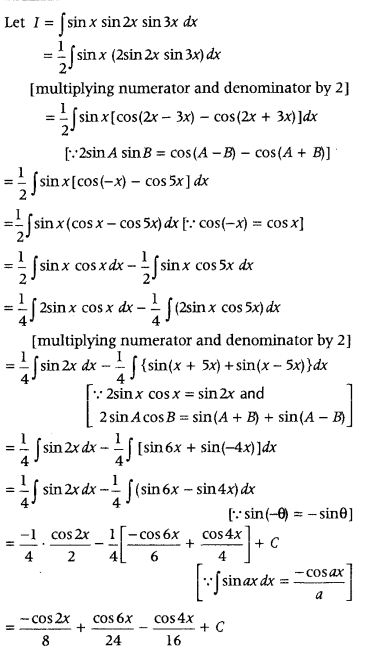

Question 87.
Evaluate ∫ 2(1−x)(1+x2) dx. (Delhi 2012)
Answer:
Here, denominator is a product of two algebraic functions. So, firstly we use partial fraction method and then integrate it.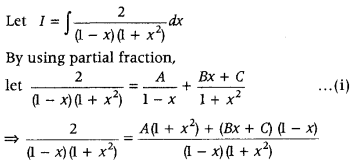

⇒ 2 = A(1 + x2) + (Bx + C)(1 – x)
⇒ 2 = A + Ax2 + Bx + C – Bx2 – Cx
⇒ 2 = (A – B)x2 + (B – C)x + (A + C)
On comparing coefficients of x2, x and constant
terms from both sides, we get
A – B = 0 ….. (ii)
B – C = 0 ….. (iii)
and A + C = 2 …… (iv)
On solving Eqs. (ii), (iii) and (iv), we get
A = 1, B = 1 and C = 1
Now, Eq. (i) become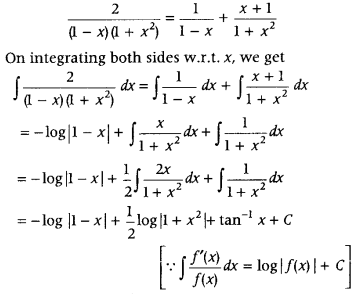

Question 88.
Evaluate ∫ (1+sinx1+cosx) ex dx (All India 2012 C)
Answer: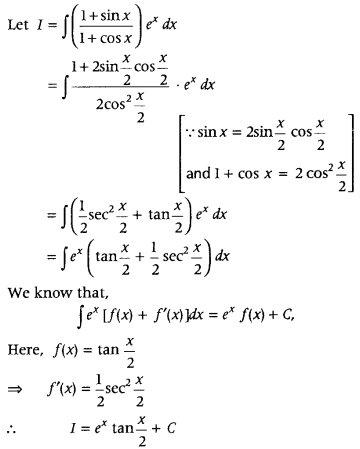

Question 89.
Evaluate ∫ (xsinx+cosx)2 dx. (All India 2012C)
Answer: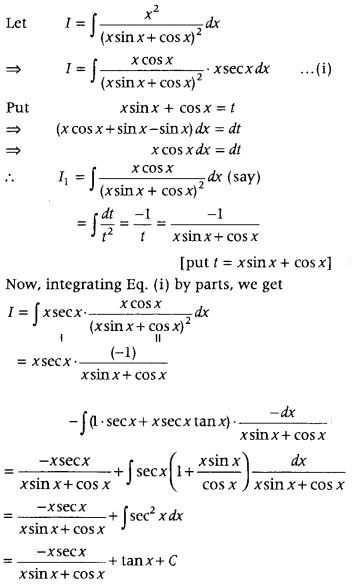

Question 90.
Evaluate ∫ e2x sin x dx. (Foreign 2011)
Answer:
15 e2x(2sin x – cos x) + C

Question 91.
Evaluate ∫3x+5x2−8x+7√ dx. (Foreign 2011)
Answer:
3x2−8x+7−−−−−−−−−√ + 17 log |(x – 4)| + (x−4)2−9−−−−−−−−−−√ + C

Question 92.
Evaluate ∫x2+4x4+16 dx. (All India 2011C)
Answer:
First, divide numerator and denominator by x2 and reduce the integrand in standard form.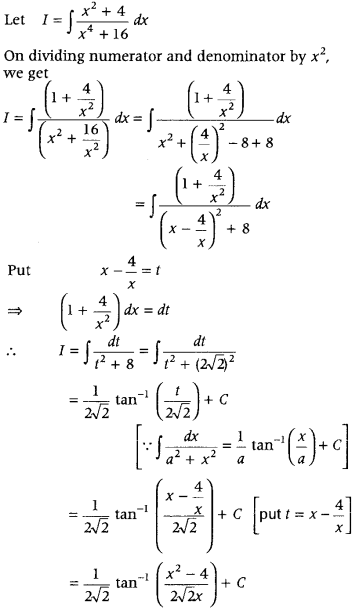

Question 93.
Evaluate ∫x2+1x4+1 dx. (Delhi 2011C)
Answer:
12√ tan-1 (x2−1x2√) + C

Question 94.
Evaluate ∫sinx−cosx dx. (Delhi 2011C)
Answer: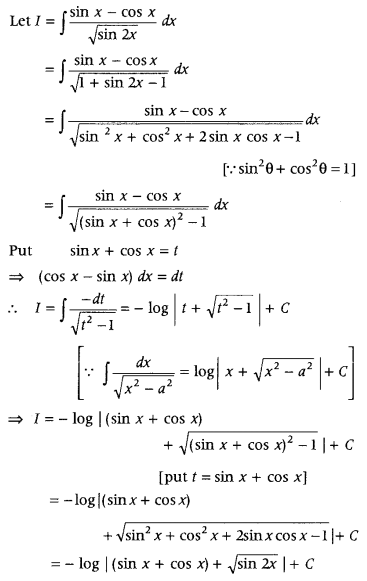

Question 95.
Evaluate ∫2x(x2+1)(x2+3) dx. (Delhi 2011)
Answer: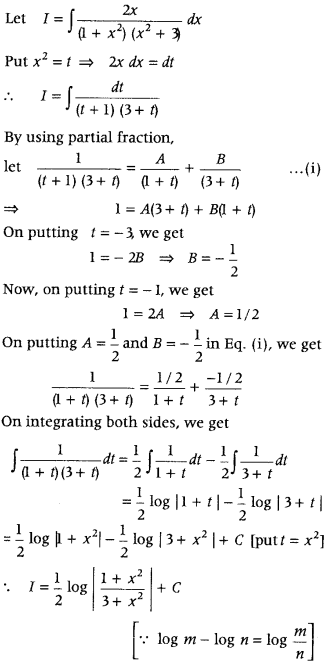

Question 96.
Evaluate ∫5x+3x2+4x+10√ dx. (Delhi 2011; All India 2010)
Answer:
5x2+4x+10−−−−−−−−−−√ – 7 log|x + 2 + x2+4x+10−−−−−−−−−−√| + C

Question 97.
Evaluate ∫ e2x (1+sin2x1+cos2x) dx. (All India 2010C)
Answer:
12 e2x tan x + C

Question 98.
Evaluate ∫dx(x2+1)(x2+2) (Delhi 2010C)
Answer:
tan-1 x – 12√ tan-1(x2√) + C

Question 99.
Evaluate ∫[log(logx)+1(logx)2] dx. (Delhi 2010C)
Answer:
Use integration by parts, i.e.

and choose 1st function with the help of ILATE procedure.

Question 100.
Evaluate ∫x+2(x−2)(x−3)√ dx. (All India 2010)
Answer: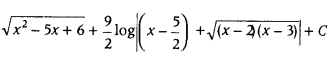

Question 101.
Evaluate ∫1−x2x(1−2x) dx. (Delhi 2010)
Answer: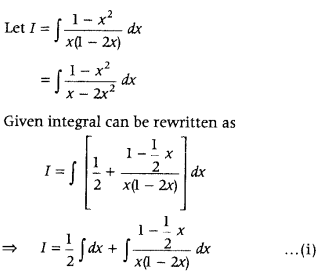

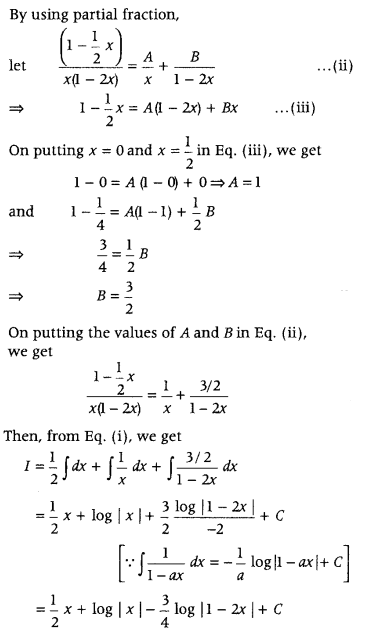
Question 102.
Evaluate ∫ ex 1−x2x(1−2x) dx. (Delhi 2010)
Answer: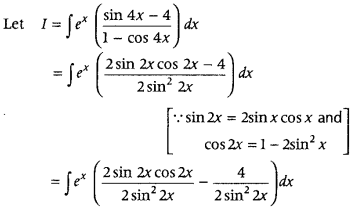

= ∫ex (cot 2x – 2 cosec2 2x) dx
We know that
∫ ex [f(x) + f'(x)] dx = ex f(x) + C
Here, f(x) = cot 2x
⇒ f'(x) = – 2 cosec2 2x
∴ I = ex cot 2x + C

Question 103.
Evaluate ∫sin4x+sin2xcos2x+cos4x dx. (All India 2014)
Answer:
First, divide numerator and denominator by cos4x to convert integrand in terms of tan x and then put tan x = t and convert integrand into standard form which can integrate easily.

Question 104.
Evaluate ∫(cotx−−−−√+tanx−−−−√) dx. (All India 2014; Delhi 2010C)
Answer:

Question 105.
Evaluate ∫cos4x+sin4x (All India 2014)
Answer:

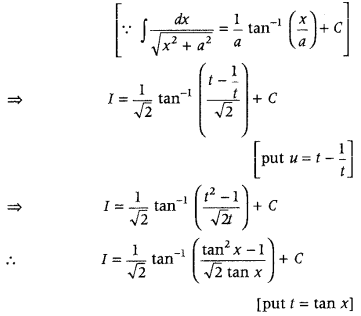
Question 106.
Find ∫x2(x2+1)(x2+4) (Delhi 2014C)
Answer:
– 13 tan-1x + 23 tan-1x2 + C

Question 107.
Find ∫sin−1x√−cos−1x√ dx, x ∈ [0, 1] (All India 2014C)
Answer:
First, use the identity sin-1 x + cos-1 x = 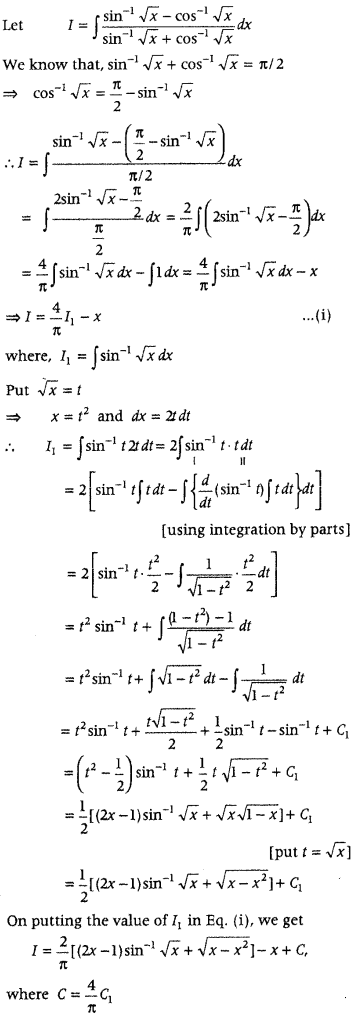π2 to convert integrand in terms of sin-1 only. Then, integrate by using substitution.

Question 108.
Find ∫x2+x+1(x+1)2(x+2) dx. (Delhi 2014C)
Answer:

⇒ x2 + x + 1 = A(x + 1) (x + 2) + B (x + 2) + C(x + 1)2
⇒ x2 + x + 1 = A(x2 + 3x + 2) + B(x + 2) + C(x2 + 2x + 1)
⇒ x2 + x + 1 = (A + C)x2 + (3A + B + 2C)x + (2A + 2B + C)
On comparing the coefficients of like powers from both sides, we get
A + C = 1,
3A + B + 2C = 1
and 2A + 2B + C = 1
On solving these equations, we get (1)
A = -2, B =1
and C = 3
From Eq. (i). we get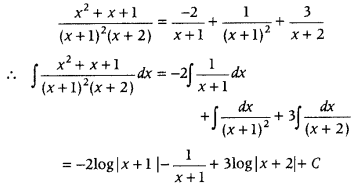

Question 109.
Find ∫x2+1√(log∣∣x2+1∣∣−2log|x|)x4 dx. (All India 2014C)
Answer: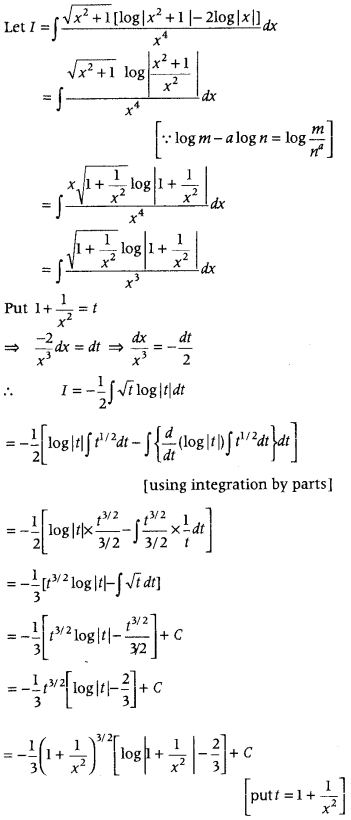

Question 110.
Evaluate ∫x2+1(x−1)2(x+3) (Delhi 2012)
Answer:

Question 111.
Evaluate ∫6x+7(x−5)(x−4)√ dx. (All India 2011)
Answer: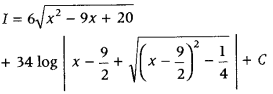

Topic 2 Definite Integrals

Question 1.
Evaluate ∫323x dx. (Delhi 2017)
Answer: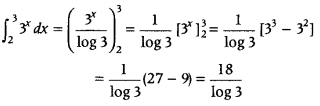

Question 2.
Evaluate ∫π/40tanx dx. (Foreign 2014)
Answer: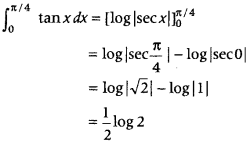

Question 3.
Evaluate ∫10xex2 dx. (Foreign 2014)
Answer: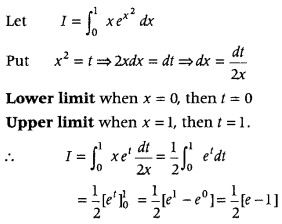

Question 4.
Evaluate ∫π/40sin2x dx. (Foreign 2014)
Answer: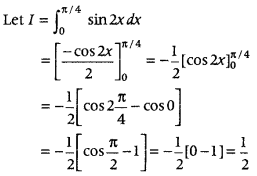

Question 5.
Evaluate ∫1011−x2√ (All India 2014C)
Answer: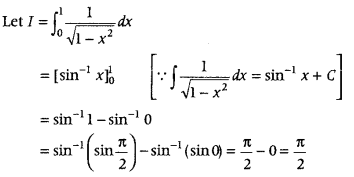

Question 6.
If ∫a014+x2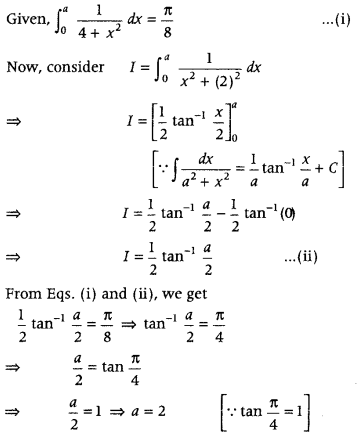dx=π8, then find the value of α. (All India 2014)
Answer:

Question 7.
If f(x) = ∫x0tsint dt, then write the value of f’ (x). (All India 2014)
Answer: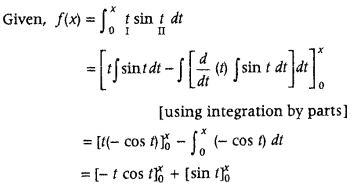

= – x cos x + 0 + sin x – 0
= sin x – x cos x
Thus. f(x) = sin x – x cos X
On differentiating both sides w.r.t. x, we get
f'(x) = cos x – [x ddx (cos x) + cos x ddx (x)] [by product rule of derivative]
= cos x – [x (- sin x) + cos x]
= cos x + x sin x – cos x = x sin x

Question 8.
Evaluate ∫42xx2+1 dx. (All India 2014)
Answer: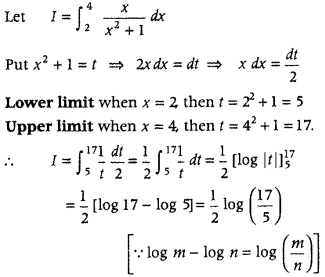

Question 9.
Evaluate ∫30dx9+x2. (Delhi 2014)
Answer: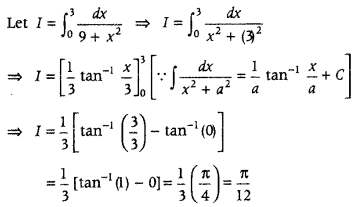

Question 10.
Evaluate ∫π/20ex(sinx−cosx) dx. (Delhi 2014)
Answer:
Let I = ∫π/20 ex (sin x – cos x) dx
I = – ∫π/20 ex (cos x – sin x) dx
Now, consider, f(x) = cos x
then f'(x) = – sin x
Now, by using ∫ex [f(x) + f'(x) dx = ex f(x) + C,
we get I = [excosx]
= – eπ/2 cos π2 + e0 cos (0)
= 0 + 1(1) = 1

Question 11.
Evaluate ∫e2edxxlogx (All India 2014)
Answer: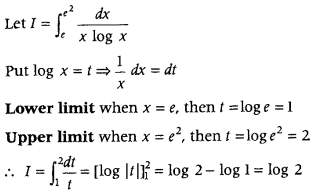

Question 12.
Evaluate ∫10tan−1x1+x2 dx. (All India 2014C)
Answer: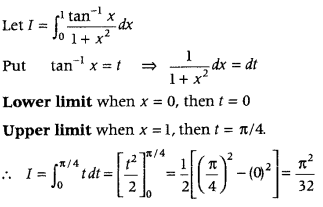

Question 13.
Evaluate ∫21x3−1x2 (India 2014C)
Answer: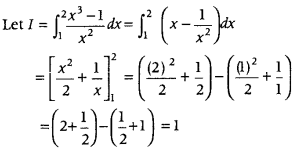

Question 14.
Evaluate ∫321x (Delhi 2012)
Answer: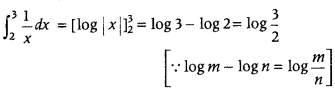

Question 15.
Evaluate ∫204−x2−−−−−√ dx. (All India 2012)
Answer: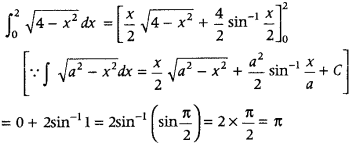

Question 16.
Write the value of ∫10ex1+e2x dx. (Delhi 2012C)
Answer:
Let I = ∫10ex1+e2x dx
= ∫10ex1+(ex)2 dx
Put ex = t ⇒ ex dx = dt
Also, when x = 0, then t = 1 and when x = 1, then t = e
Now, I = ∫e1dt1+t2=(tan−1t)e1
= tan-1 e – tan-1 1 = tan-1(e−11+e)

Question 17.
Evaluate ∫3√1dx1+x2 (Foregin 2011)
Answer: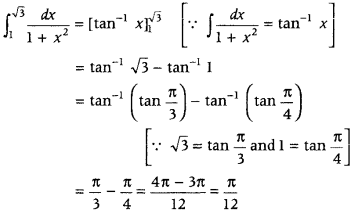

Question 18.
Evaluate ∫102x1+x2 dx. (All India 2011C, 2008)
Answer:
log 2

Question 19.
Evaluate ∫1011+x2 dx. (Delhi 2011C)
Answer:
π4

Question 20.
Evaluate ∫π/4−π/4sin3x dx. (Delhi 2010C)
Answer:
Use, the property ∫a−a f(x)dx = 0, if f(x) is an odd function
let I = ∫π/4−π/4 sin3 x dx
consider, f(x) = sin3x. Then, f(-x) = sin3(-x)
= (-sinx)3 = -sin3x = -f(x)
⇒ f(x) is an odd function.
Thus, the given integrand is an odd function.
∴ I = 0
[∵ ∫a−a f(x)dx = 0, if f(x) is an odd function]

Question 21.
Write the value of the following integral
∫π/2−π/2 sin5 x dx. (All India 2010)
Answer:
0

Question 22.
Evaluate ∫2−1|x|x dx. (Delhi 2019)
Answer:
Let I = ∫π−π (1 – x2) sin x cos2 x dx
Again, let f(x) = (1 – x2) sin x cos2 x
∴ f(- x) = [1 – (- x)2] sin (- x) cos2(- x)
= (1 – x2) (- sin x) cos2 x
= – (1 – x2) sin x cos2x
= – f(x)
∴ f(x) is odd function
∴ I = 0
[∵ ∫a−a f(x) dx = 0, if f(x) is odd function] (1)

Question 23.
Evaluate ∫2−1|x|x dx. (Delhi 2019)
Answer: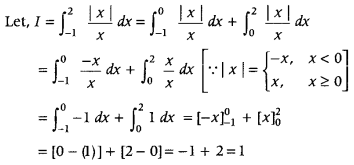

Question 24.
Prove that ∫a0f(x) dx = ∫a0f(a−x) dx, hence evaluate ∫π0xsinx1+cos2x. (Delhi 2019)
Answer: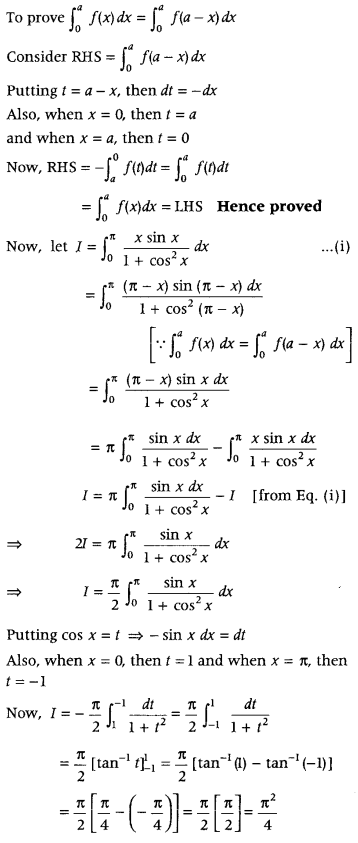

Question 25.
Prove that ∫a0f(x) dx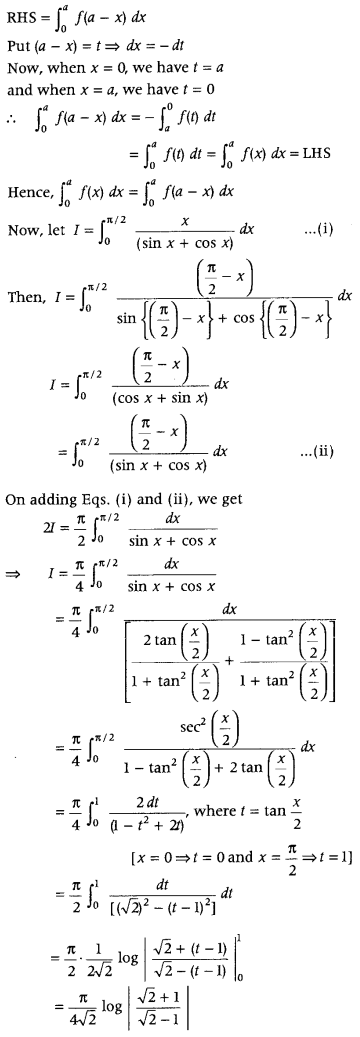 = ∫a0f(a−x) dx. and hence evaluate ∫π/20xsinx+cosx dx. (All India 2019)
Answer:

Question 26.
Evaluate ∫∞1 ( |x – 1| + |x – 2| + |x – 4|) dx. (All India 2017; Delhi 2011C)
Answer:
Here, |x – 1|, |x – 2| and |x – 4| occurs.
Now, define the absolute function as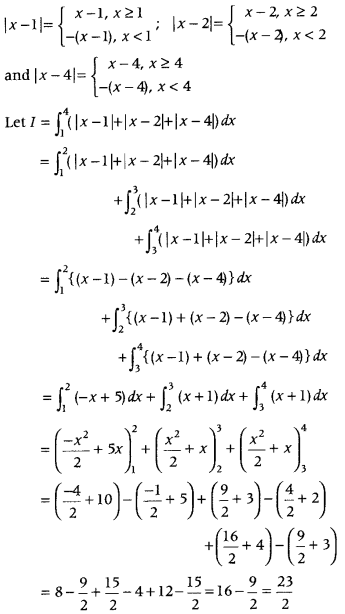

Question 27.
Evaluate ∫π0xsinx1+cos2x dx. (Delhi 2017, All India 2013, 2012 2011C, 2009C, 2008)
Answer: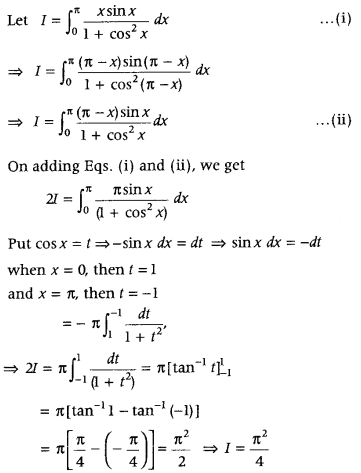

Question 28.
Evaluate ∫π0xtanxsecx+tanx dx. (All India 2017)
Answer: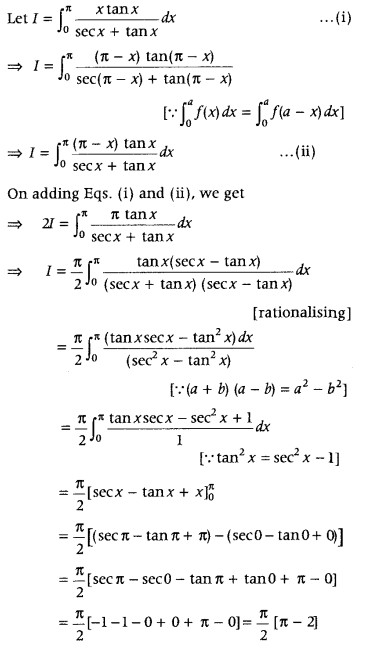

Question 29.
Evaluate ∫2−1∣∣x3−x∣∣ dx. (Delhi 2016; All India 2010)
Answer:
First, define the absolute function in the given interval and then integrate it.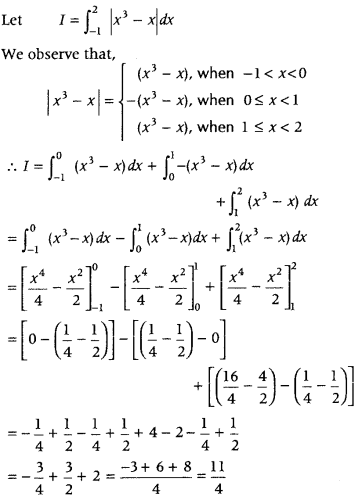

Question 30.
Evaluate ∫π0e2x⋅sin(π4+x) dx. (Delhi 2015)
Answer: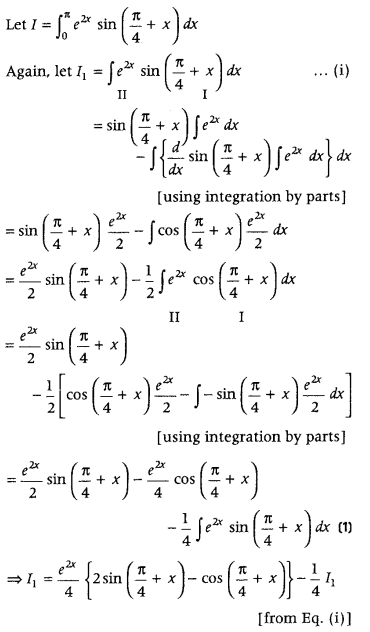

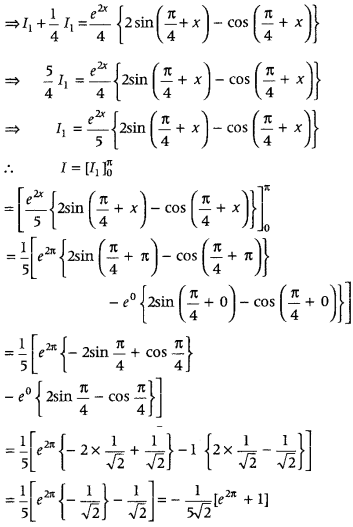
Question 31.
Evaluate ∫2−2x21+5x dx. (All India 2016)
Answer: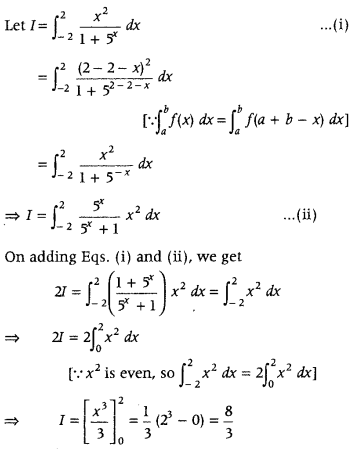

Question 32.
Evaluate ∫3/20|xcosπx| dx (All India 2016)
Answer:

Question 33.
Evaluate ∫π0x1+sinαsinx dx. (Foreign 2016)
Answer: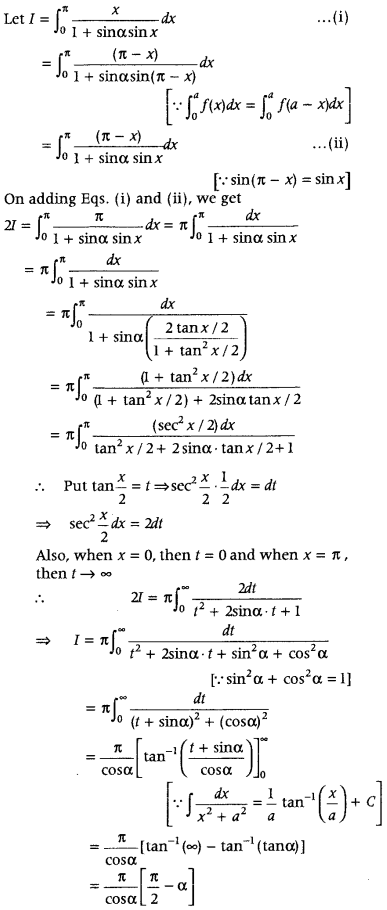

Question 34.
Evaluate ∫π−π(cosax−sinbx)2 dx. (Delhi 2015)
Answer: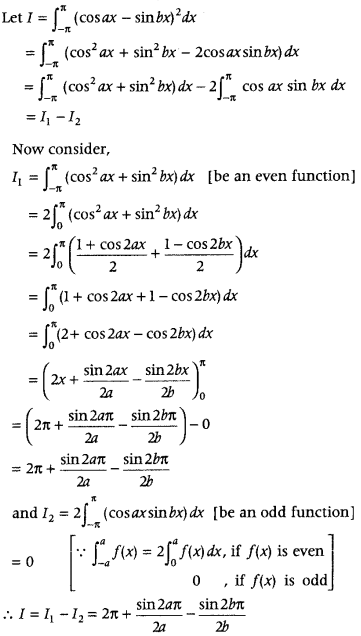

Question 35.
Find ∫π/40dxcos3x2sin2x√ (All India 2015)
Answer:

Question 36.
Evaluate ∫π/2−π/2cosx1+ex dx. (Foreign 2015)
Answer: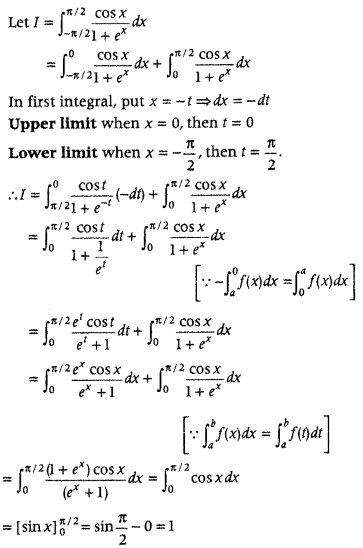

Question 37.
Evaluate ∫π/40log(1+tanx) log (1 + tan x) dx. (All India 2015C, 2010; Delhi 2013C)
Answer:

Question 38.
Evaluate ∫π/3π/6sinx+cosxsin2x√ dx. (All India 2014C; Delhi 2011)
Answer: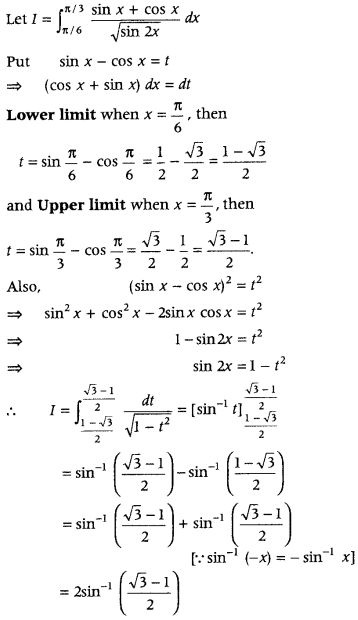

Question 39.
Evaluate ∫π/20 x2 sin x dx. (Delhi 2014C)
Answer:
Let I = ∫π/20 x2 sin x dx

= – x2 cos x + 2[x (sin x) – ∫1 . (sin x) dx]
[using integration by parts]
= – x2 cos x + 2(sin x + cos x)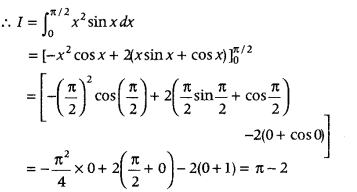

Question 40.
Prove that
∫π/20sin2xsinx+cosx dx = 12√ log(√2 + 1). (All India 2014C)
Answer: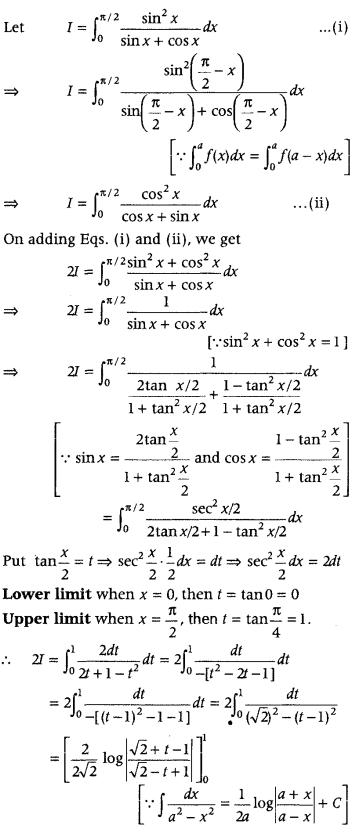

Question 41.
Evaluate ∫52 [|x – 2| + |x – 3| + |x – 5|] dx. (Delhi 2013)
Answer:
First, we redefined the integrand of the integral between the given limits (2, 5). After that integrate and simplify it.
For, 2 ≤ x < 5, |x – 2| = (x – 2)
2 ≤ x < 3, |x – 3| = – (x – 3)
3 ≤ x < 5, |x – 3| = (x – 3)
and 2 ≤ x < 5, |x – 5| = (5 – x)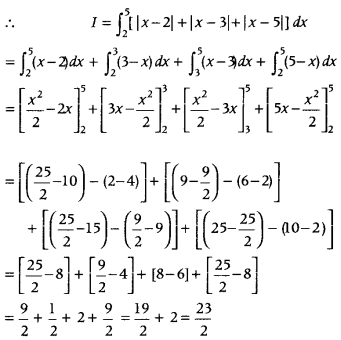

Question 42.
Evaluate ∫40 [|x| + |x – 2| + |x – 4|] dx. (Delhi 2013)
Answer:
Let I = ∫40 [|x| + |x – 2| + |x – 4|] dx
Here, redefined the given integrand in given interval (0, 4).
For, 0 < x < 4, |x| = x
0 < x ≤ 2, |x – 2| = – (x – 2)
2 ≤ x < 4, |x – 2| = (x – 2)
0 < x < 4, |x – 4| = – (x – 4)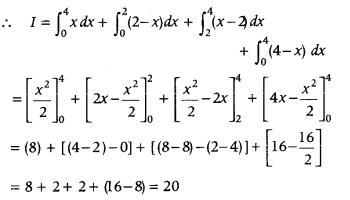

Question 43.
Evaluate ∫13 [|x – 1| + |x – 2| + |x – 3|]dx. (Delhi 2013)
Answer:
5

Question 44.
Evaluate ∫2π011+esinx dx (All India 2013)
Answer: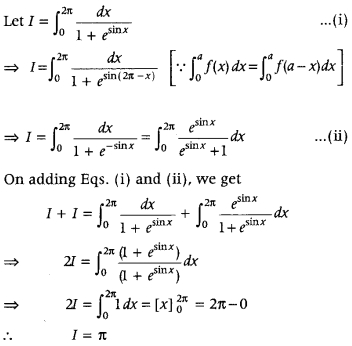

Question 45.
Evaluate ∫10x4+1x2+1 dx. (All India 2011C)
Answer:
Here, the power of numerator is greater than the power of denominator. So, first we add and subtract 1 in numerator and use formula (a2 – b2) = (a – b) (a + b)to simplify it and then integrate it.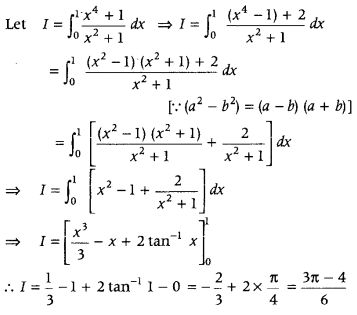

Question 46.
Evaluate ∫π/20x+sinx1+cosx dx (All India 2011)
Answer: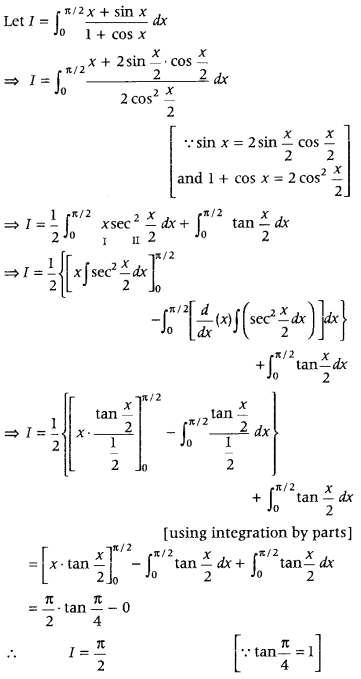

Question 47.
Evaluate ∫215x2x2+4x+3 dx. (All India 2011)
Answer:
Here, the power of numerator and denominator are same. So, first we divide numerator by denominator and write integrand in the form (RD+Q), where R = remainder, Q = quotient and D = divisor. Now, integrate it easily by using partial fraction.

Question 48.
Evaluate ∫10log|1+x|1+x2 dx. (All India 2011C)
Answer: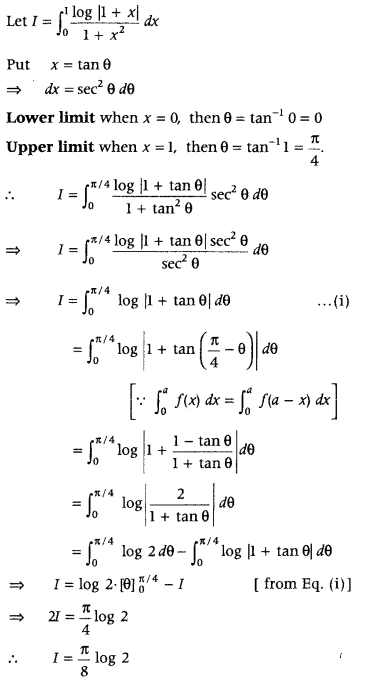

Question 49.
Evaluate ∫10log∣∣1x−1∣∣ dx. (All India 2011)
Answer:

Question 50.
Evaluate ∫π0x1+sinx dx. (Delhi 2010)
Answer:

Question 51.
Find ∫13 (x2 + 2 + e2x) dx as the limit of sums. (All India 2019)
Answer:
We have ∫13 (x2 + 2 + e2x) dx
On comparing with ∫ba f(x) , we get
a = 1, b = 3, nh = 3 – 1 = 2,
f(x) = x2 + 2 + e2x
Clearly, f(1) = 12 + 2 + e2 × 1 = 3 + e2
f(1 + h) = (1 + h)2 + 2 + e2(1 + h)
= 1 + 2h + h2 + 2 + e2 + 2h
= 3 + 2h + h2 + e2 ∙ e2h
f(1 + 2h) = (1 + 2h)2 + 2 + e2(1 + 2h)
= 1 + 4h + 4h2 + 2 + e2 + 4k
= 3 + 4h + 4h2 + e2 ∙ e4h
f(1 + (n – 1) h) = (1 + (n – 1) h)2 + 2 + e2(1 + (n – 1)h)
= 1 + 2(n – 1)h + (n – 1)2 h2 + 2 + e2 + 2(n – 1)h
= 3 + 2(n – 1) h + (n – 1)2 h2 + e2 ∙ e2(n – 1)∙h
∴ f(1) + f(1 + h) + f(a + 2h) + …… + f(1 + (n – 1)h)
= (3 + 3 + 3 + …… + 3 + 2h(1 + 2 + 3 + …… + (n – 1)2) + h2(12 + 22 + 32 + …… + (n – 1)2) + e2 (1 + e2h + ……. + e2h(n – 1))

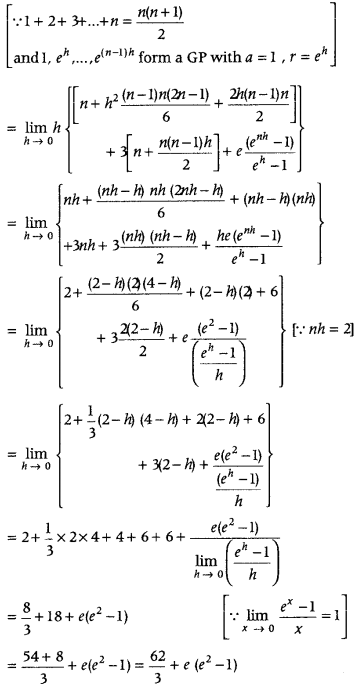
Question 52.
Evaluate ∫π/40sinx+cosx16+9sin2x (CBSE 2018)
Answer: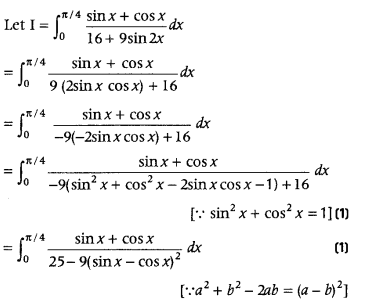

put sin x – cos x = t ⇒ (cos x + sin x)dx = dt
Also, when, x = 0, then t = -1 and when, x = 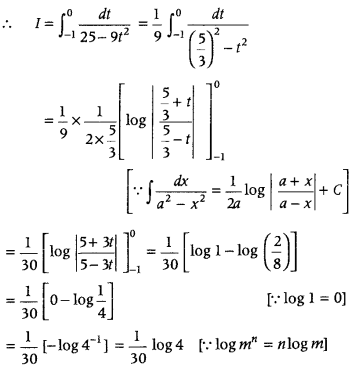π4, then t = 0

Question 53.
Evaluate ∫31 (x2 + 3x + ex) dx as the limit of the sum. (CBSE 2019)
Answer:

Question 54.
Evaluate ∫31 (3x2 + 2x + 1) dx as the limit of a sum. (CBSE 2018C)
Answer:
Here, a = 1, b = 3, f(x) = 3x2 + 2x + 1
Now, nh = b – a = 3 – 1 = 2

Question 55.
Evaluate ∫π/20xsinxcosxsin4x+cos4x dx. (Delhi 2014, 2011; AIl India 2010C)
Answer:

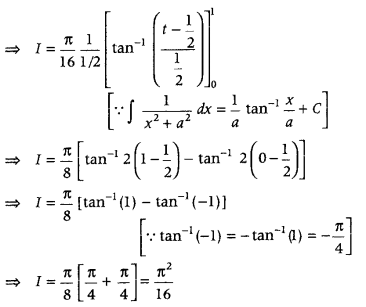
Question 56.
Evaluate ∫31 (e2 – 3x + x2 + 1)dx as a limit of a sum. (Delhi 2015)
Answer: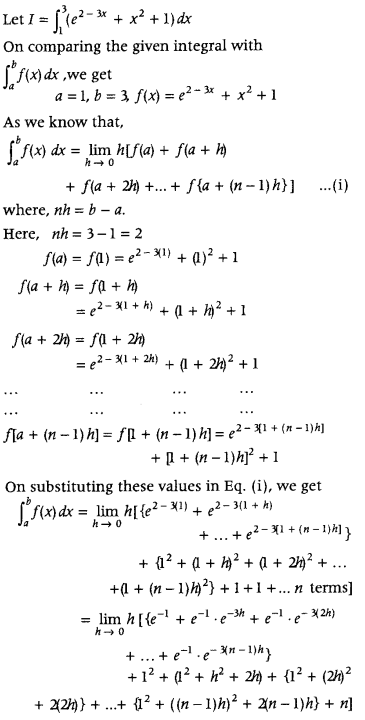

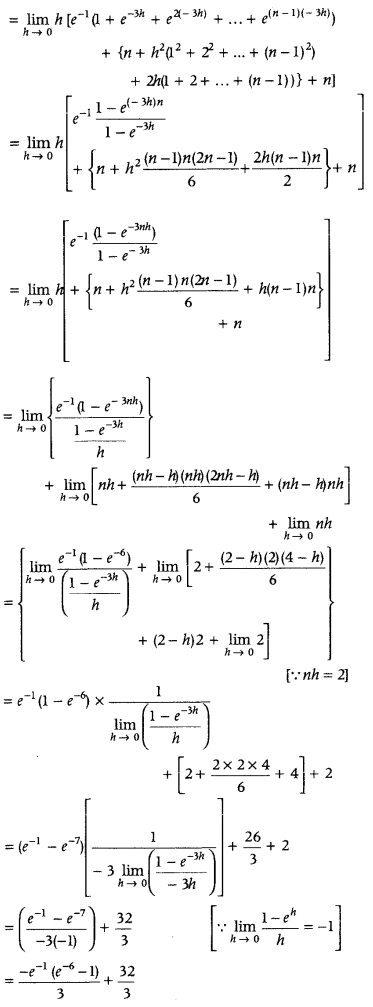
Question 57.
Evaluate ∫π/40sinx+cosx9+16sin2x dx. (Foreign 2014; Delhi 2014C 2011)
Answer:
First, convert the denominator in the form of (cos x – sin x), then put cos x – sin x = t and simplify it.

Question 58.
Evaluate ∫π0xa2cos2x+b2sin2x dx. (Foreign 2014; All India 2008)
Answer:

Question 59.
Evaluate ∫π0xtanxsecx+tanx dx. (Foreign 2014; Delhi 2014C, 2010, 2008; All India 2008)
Answer:

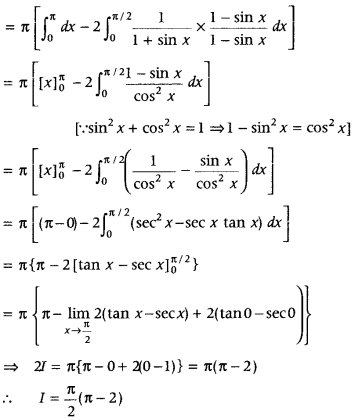
Question 60.
Evaluate ∫π/3π/6dx1+cotx√. (Delhi 2014)
Answer:

Question 61.
Evaluate ∫31 (3x2 + 1) dx by the method of limit of sum. (Delhi 2014C)
Answer:
Im limit of a sum, use the relation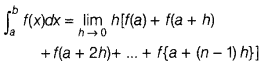

Question 62.
Evaluate ∫31 (2x2 + 5x) dx as a limit of a sum. (Delhi 2012)
Answer:
we know that, by limit of a sum, we have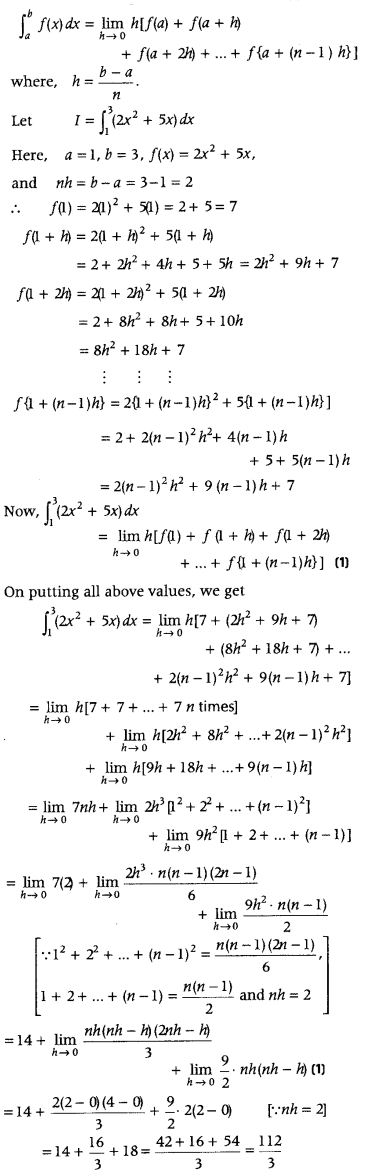

Question 62.
Evaluate ∫31 (2x2 + 5x) dx as a limit of a sum. (Delhi 2012)
Answer:
we know that, by limit of a sum, we have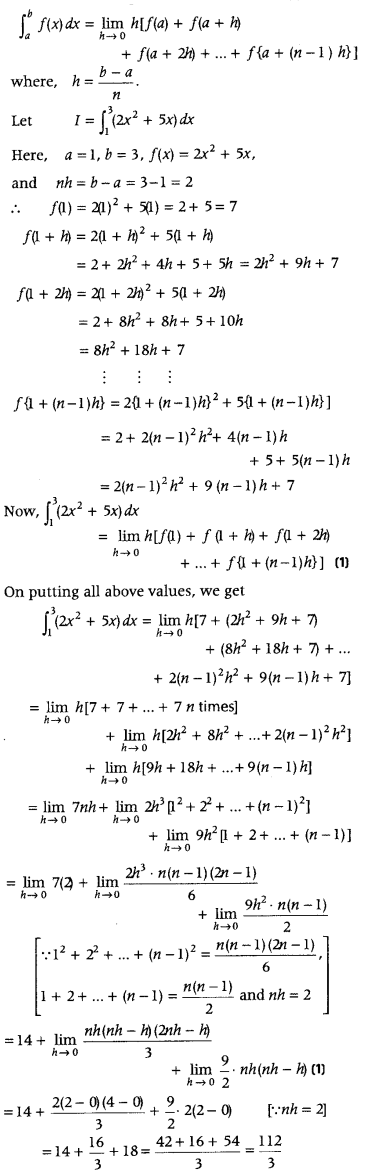

Question 63.
Prove that ∫π/40(tanx−−−−√+cotx−−−−√) dx = √2 ∙ π2 (Delhi 2012)
Answer: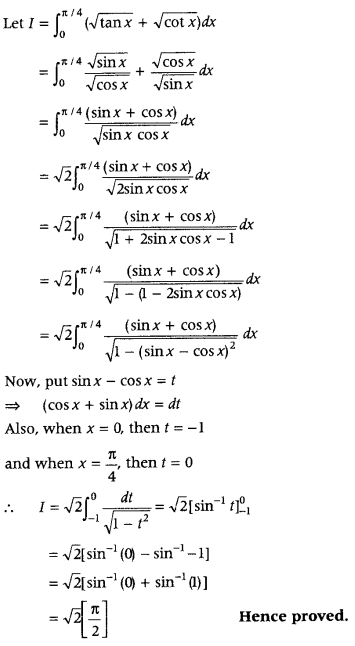

Question 64
∫π/2π/4cos2x⋅log(sinx) dx (Delhi 2012C)
Answer: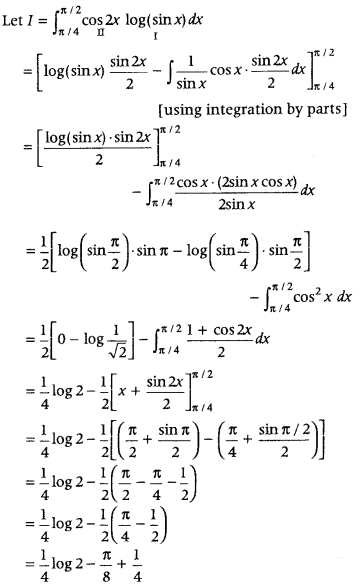

Question 65.
Evaluate ∫π0xtanxsecx⋅cosecx dx. (Delhi 2011C 2008; All India 2009)
Answer: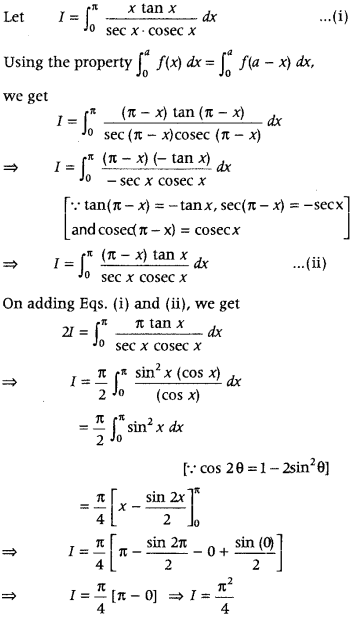

Question 66.
Evaluate ∫π/202sinxcosxtan−1(sinx) dx. (Delhi 2011)
Answer: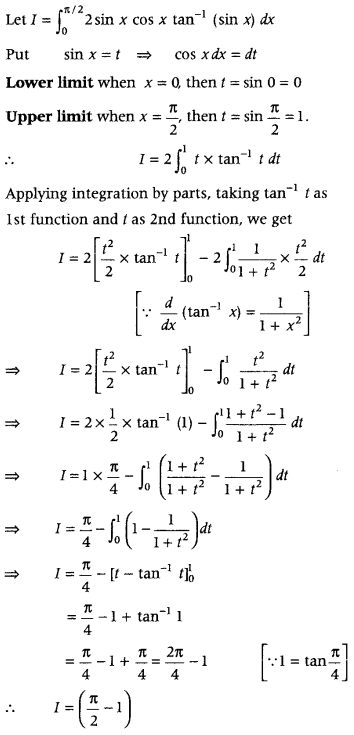

Question 67.
Evaluate ∫π/3π/6dx1+tanx√ (All lndia 2011)
Answer:
π12

Question 68.
Evaluate ∫41 (x2 – x) dx as a limit of a sum. (Delhi 2011, 2010)
Answer:
Given integral is ∫41 (x2 – x) dx
Here, a = 1, b = 4, f(x) = x2—x
and nh = b – a = 4 – 1 = 3
Now, f(a) = f(1) = (1)2 – (1) = 1 – 1 = 0
f(a + h) = f(1 + h)
= (1 + h)2 – (1 + h)
= 1 + h2 + 2h – 1 – h
= h2 + h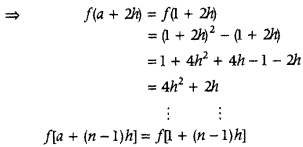

= [1 + (n – 1)h]2 – (1 + (n – 1)h]
= 1 + (n – 1)2 h2 + 2(n – 1)h – 1 – (n – 1)h
= (n – 1)2 h2 + (n – 1)h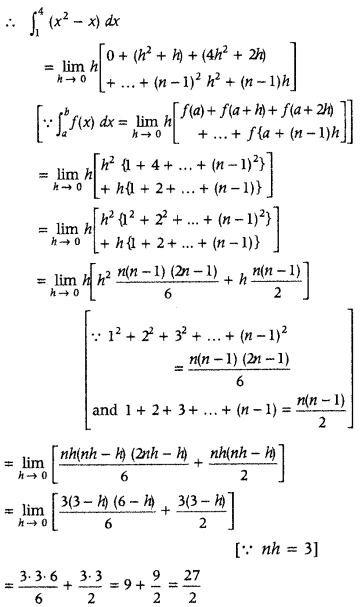

Question 69.
Evaluate ∫20 (3x2 – 2) dx as a limit of a sum. (All India 2011C)
Answer:
4

Question 70.
Evaluate ∫20 (x2 – x) dx as a limit of a sum. (Delhi 2011C)
Answer:
Hint: Here, a = 0, b = 2, nh = 2
23

Question 71.
Evaluate ∫13 (2x2 + 3) dx as a limit of a sum. (Delhi 2010, 2009C)
Answer:
703

Question 72.
Evaluate ∫12 (x2 + 5x) dx as a limit of a sum. (Delhi 2010C)
Answer:
596

Question 73.
Evaluate ∫13 (3x2 + 2x) dx as a limit of a sum. (Delhi 2010)
Answer:
34